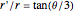Trisecting an Angle Using Tschirnhaus's Cubic
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
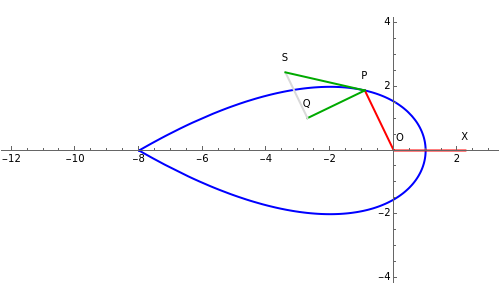
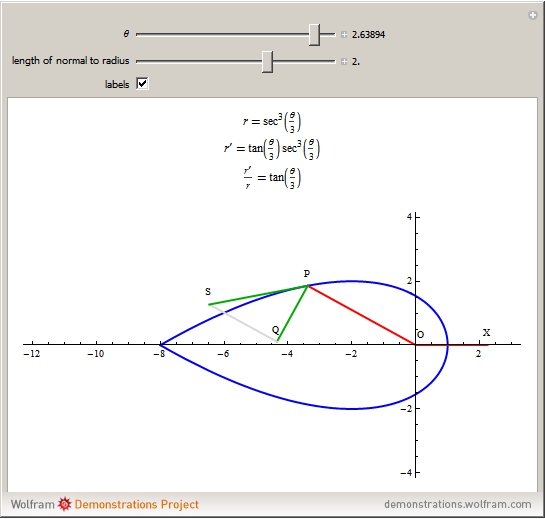
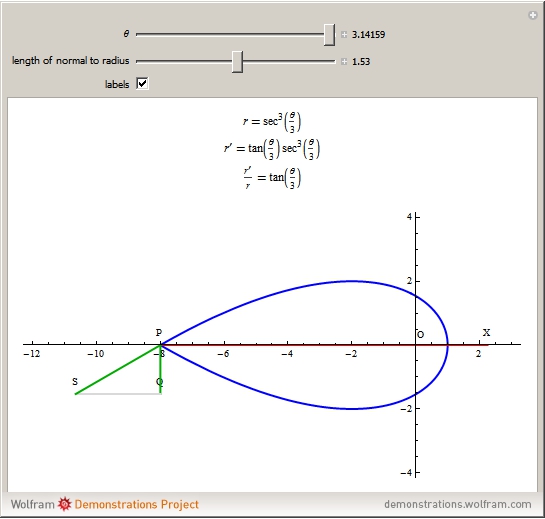
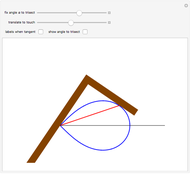
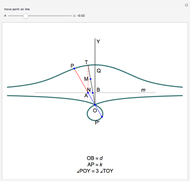
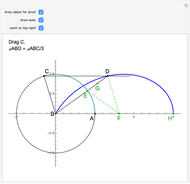
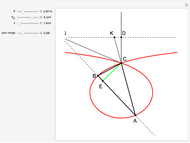
This Demonstration illustrates a property of Tschirnhaus's cubic, which has polar equation 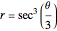 . Namely, that the angle
. Namely, that the angle  between the tangent
between the tangent 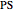 and the normal
and the normal  to the radius vector
to the radius vector 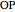 at a given point
at a given point  on the curve is one-third of the polar angle
on the curve is one-third of the polar angle 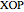 of the point.
of the point.
Contributed by: Izidor Hafner (January 2013)
Open content licensed under CC BY-NC-SA
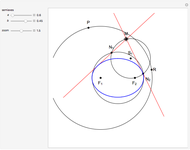
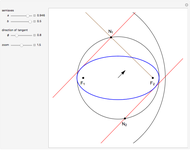
Snapshots
Details
The curve is also known as Catalan's trisectrix or l'Hospital's cubic.
Permanent Citation