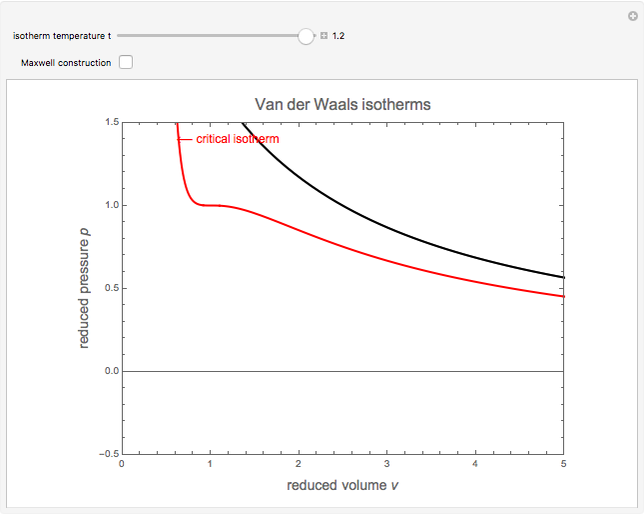
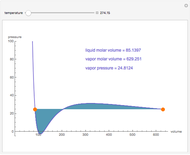
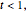Van der Waals Isotherms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
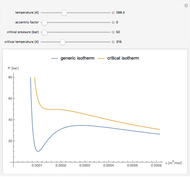
The Van der Waals equation of state for one mole of an imperfect fluid reads 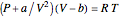 . The critical constants are predicted to be
. The critical constants are predicted to be 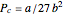 ,
,  ,
, 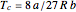 . The Van der Waals equation can be recast in the form of a universal reduced equation of state
. The Van der Waals equation can be recast in the form of a universal reduced equation of state 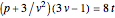 in terms of reduced variables
in terms of reduced variables 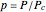 ,
, 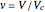 ,
, 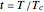 . Isotherms where
. Isotherms where 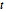 is constant can be plotted on the
is constant can be plotted on the  versus
versus 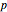 diagram using the slider for values of
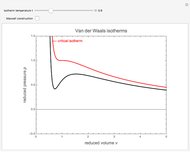
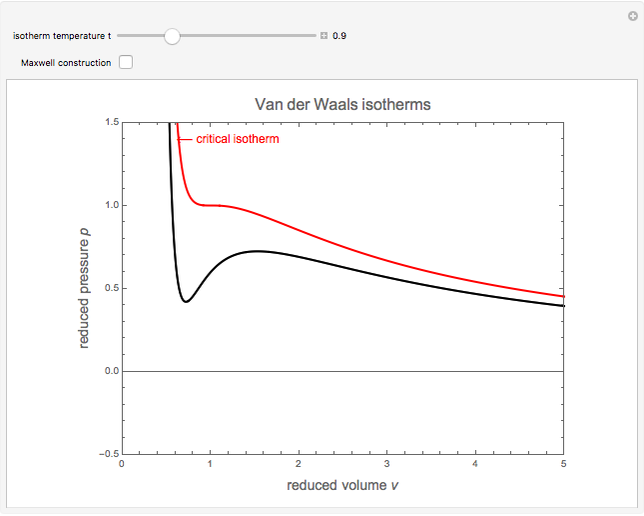
diagram using the slider for values of  between 0.80 and 1.20. The critical isotherm
between 0.80 and 1.20. The critical isotherm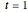 is shown in red.
is shown in red.
Contributed by: S. M. Blinder (February 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: isotherm for 
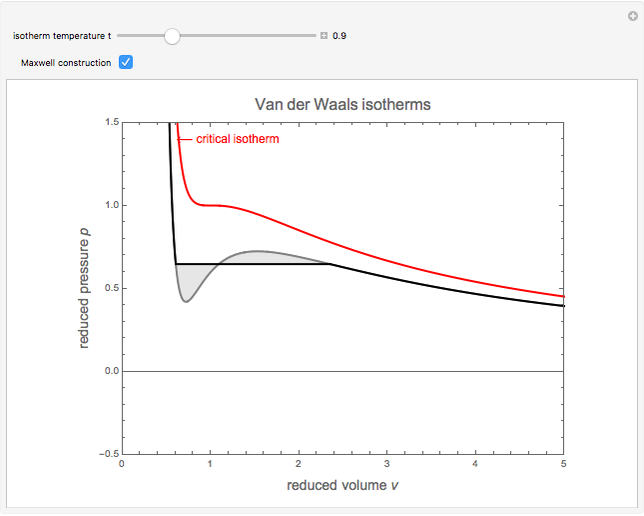
Snapshot 2: isotherm for  , showing Maxwell construction
, showing Maxwell construction
Snapshot 3: isotherm for 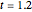 , approaching the hyperbolic shape of an ideal-gas isotherm
, approaching the hyperbolic shape of an ideal-gas isotherm
The Van der Waals equation is discussed in all physical chemistry texts. See, for example:
P. W. Atkins and J. de Paula, Physical Chemistry, 8th ed., New York: Oxford University Press, 2006.
S. M. Blinder, Advanced Physical Chemistry: A Survey of Modern Theoretical Principles, New York: Macmillan, 1969.
Permanent Citation