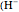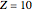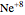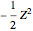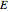Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Van Vleck's Model of the Helium Atom in the Old Quantum Theory

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

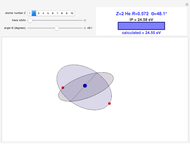
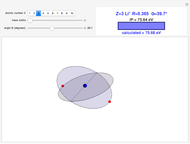
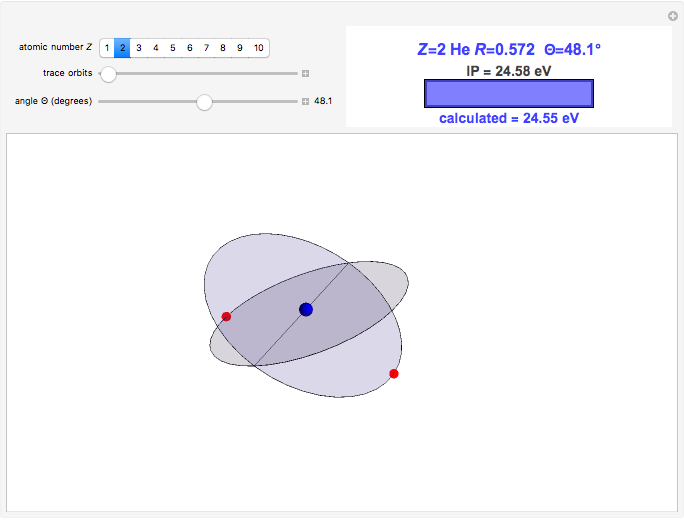
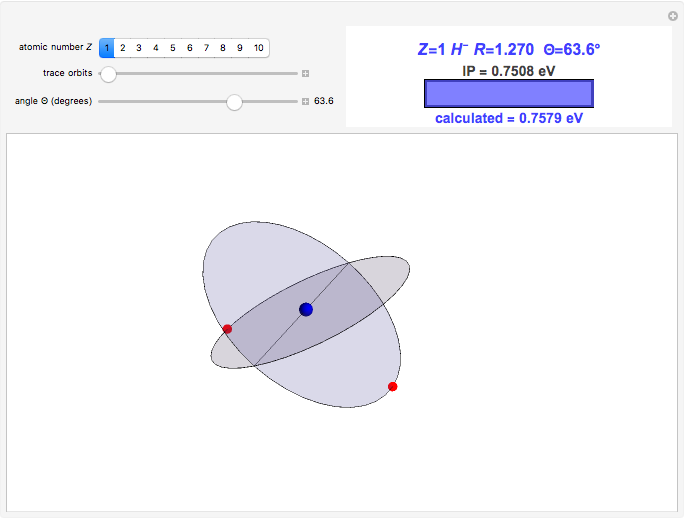
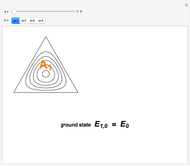
Niels Bohr's 1913 model of the hydrogen atom, now known as the old quantum theory (OQT), was a spectacular success in accounting for the spectrum of atomic hydrogen and introducing the concept of energy-level quantization. However, many valiant attempts to extend the Bohr model to the helium atom and beyond met with miserable failure, necessarily awaiting the development of quantum mechanics in 1925–1926. This Demonstration reproduces probably the most creditable OQT model of the helium atom, which was proposed in the doctoral dissertation of J. H. Van Vleck in 1922 [1, 2].

[more]

According to this model, the two electrons in helium follow elliptical orbits around the nucleus, in intersecting planes mutually separated by a dihedral angle of , something of the order of 60°. The classical equations of motion, a three-body problem, cannot be solved in closed form, but reasonable approximations are possible. With appropriate choices of the orbital radius and angle of inclination, the experimental ionization energy IP of the atom can be reproduced.

Beyond the original work of Van Vleck, consider the isoelectronic series of two electron atomic species from ) to (). The corresponding singly ionized, one-electron systems can be solved exactly to give energies of hartrees. Thus IP = eV, where is the two-electron energy in hartrees.

For a given atomic number , you can vary the angle to fit the experimental ionization energy.

[less]

Contributed by: S. M. Blinder (December 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

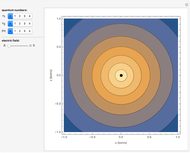
In this model for the motion of the two electrons in atomic helium, the orbits trace out ellipses representing two oblique cross-sections of a cylinder of radius , mutually intersecting at an angle . The two electrons, in cylindrical coordinates, are specified by:

.

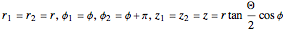The kinetic energy is given by . Each electron-nuclear distance equals 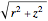, while the electron-electron distance equals , thus giving a potential energy, in atomic units, .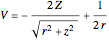

The Lagrangian

leads to the equations of motion:

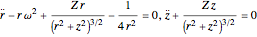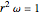, , where .

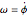Earlier suggestions of a "crossed-orbit" model of the helium atom were made by Neils Bohr and his assistant, H. A. Kramers, as well as by E. C. Kemble, who was Van Vleck's doctoral advisor. The resulting dissertation is often considered the first American PhD thesis purely devoted to a topic in theoretical quantum physics. A personal note: Nobel laureate J. H. Van Vleck [3] was co-advisor for my own doctoral dissertation.

References

[1] J. H. Van Vleck, "A Critical Study of Possible Models of the Normal Helium Atom," PhD dissertation, Harvard University, 1922.

[2] J. H. Van Vleck, "The Normal Helium Atom and Its Relation to the Quantum Theory," Philosophical Magazine 44(263), 1924 pp. 842–869. doi.org/10.1080/14786441208562559.

[3] Wikipedia. "John Hasbrouck Van Vleck." (Dec 4, 2017) en.wikipedia.org/wiki/John_Hasbrouck_Van _Vleck.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send