Wavelet Shrinkage Denoising

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
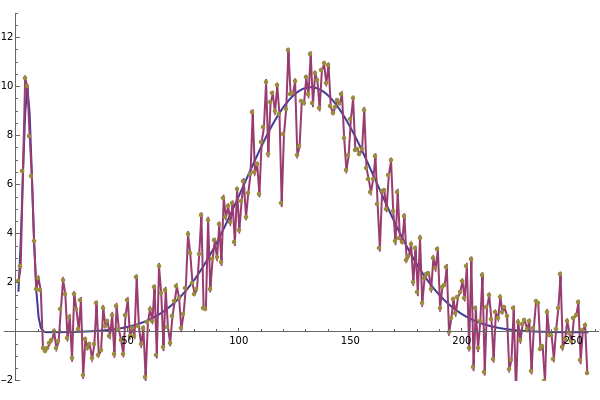
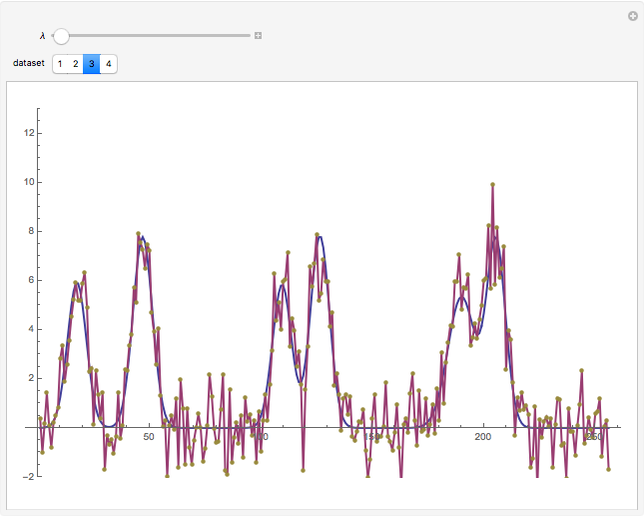
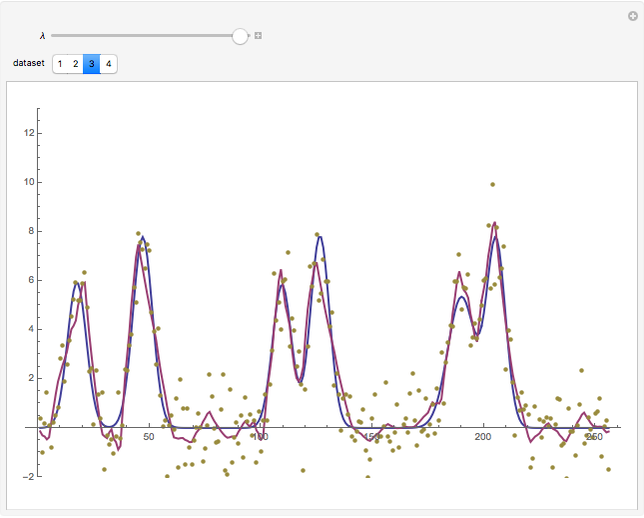
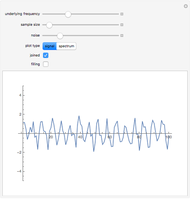
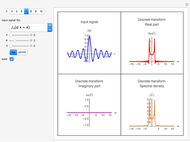
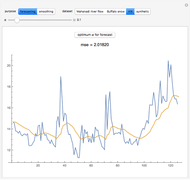
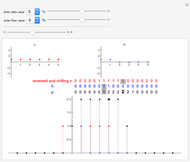
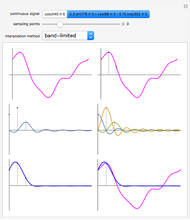
Three iterations of the discrete wavelet transform are computed using the Daubechies six-term filter. The wavelet transform splits the data into lowpass (approximation) portions and highpass (detail) portions. Wavelet shrinkage reduces the magnitude of terms in the highpass portions. Finally, the wavelet transform is inverted to get the denoised version of the data. The blue and purple curves are the plots of the clean and denoised data (points joined) and the tan points are the plot of the noisy data. The amount of shrinkage is controlled by the tolerance, 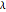 .
.
Contributed by: Bruce Atwood (Beloit College) (March 2011)
After work by: Patrick Van Fleet (University of St. Thomas)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The terms "smoothing" and "denoising" are sometimes used interchangeably, but students should look at the related Demonstration, Data Smoothing, and ask themselves what the differences are between moving averages and wavelet shrinkage. Are some moving weighted averages just special cases of wavelet shrinkage?
Setting 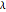 to the universal threshold (about 3.3 for these datasets and noise level) gives the output for the VisuShrink wavelet shrinkage algorithm. For more information on wavelet transformations and applications to denoising, see P. J. Van Fleet, Discrete Wavelet Transformations, Hoboken, NJ: John Wiley & Sons, Inc., 2008.
to the universal threshold (about 3.3 for these datasets and noise level) gives the output for the VisuShrink wavelet shrinkage algorithm. For more information on wavelet transformations and applications to denoising, see P. J. Van Fleet, Discrete Wavelet Transformations, Hoboken, NJ: John Wiley & Sons, Inc., 2008.
Permanent Citation