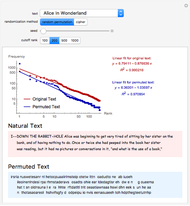
Zipf's Law for Natural and Random Texts

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
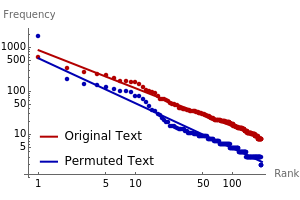
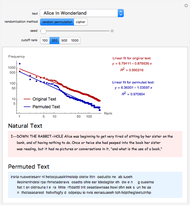
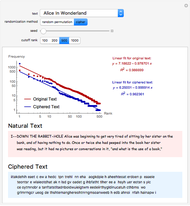
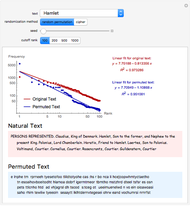
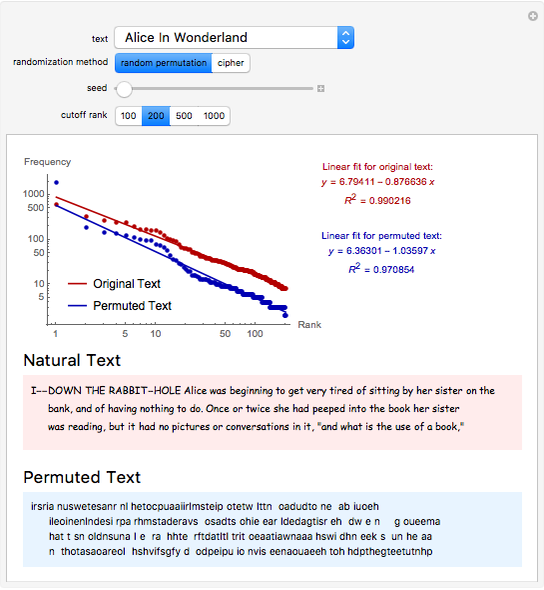
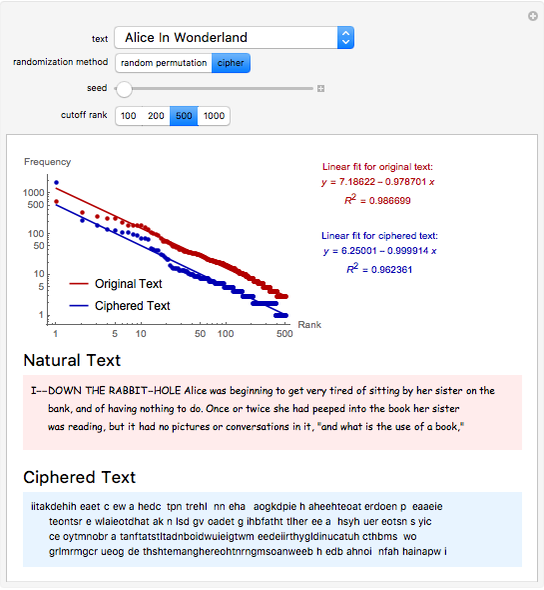
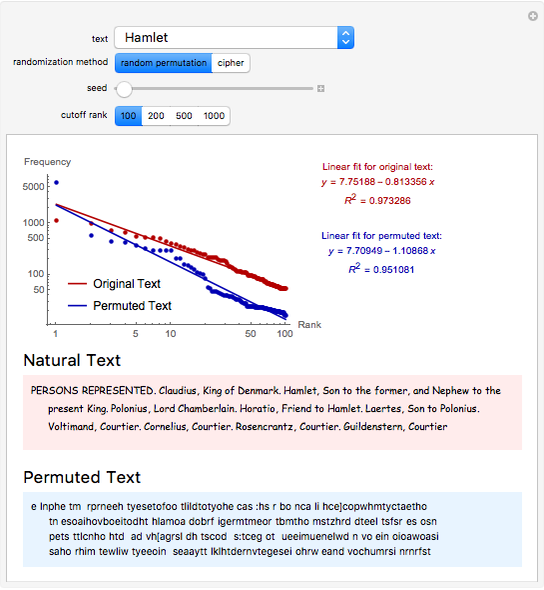
Zipf's law states that the frequency of words in natural languages is approximately inversely proportional to their rank (or frequency of use). This Demonstration compares Zipf's law for natural language texts to that of randomized versions of these texts, obtained by either randomly permuting all characters (including spaces) of the text, or by applying a transposition cipher to the text. In most cases, the fit of Zipf's law for the randomized versions is similar to that of the original texts.
Contributed by: Daniyar Omarov (September 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
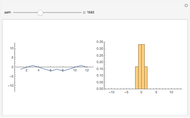
The general form of Zipf's law states that 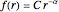 , or equivalently
, or equivalently 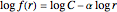 , where
, where  is the rank of a word,
is the rank of a word, 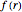 is the frequency and
is the frequency and  is a parameter. This Demonstration shows a log-log plot of the data points
is a parameter. This Demonstration shows a log-log plot of the data points 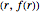 for a given text up to a user-defined cutoff rank
for a given text up to a user-defined cutoff rank  , along with the best-fit line obtained by the least-squares method. It also gives the
, along with the best-fit line obtained by the least-squares method. It also gives the 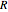 -squared statistic for the fit; an
-squared statistic for the fit; an 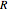 -squared value close to 1 indicates a good fit.
-squared value close to 1 indicates a good fit.
The randomized versions of the text were obtained by either randomly permuting the characters and spaces in the original text, or by applying a column transposition cipher to the text. In the column transposition method, the ciphered text is constructed by writing out the text in rows of a given length, and then reading it back in column by column. The code uses 66 as the row length in this method. For similar choices of row length, the results would be similar.
Other methods of randomization and of measuring the fit to Zipf's law have been considered in [1] and [2], which arrived at opposite conclusions. This Demonstration suggests that randomized texts created with the same letter frequencies of a natural text satisfy Zipf's law with comparable accuracy, provided the same cutoff values for the ranks are used.
Similar power-law distributions occur in rankings other than those involving language including sizes, populations, incomes and others.
References
[1] R. Ferrer-i-Cancho and B. Elvevåg, "Random Texts Do Not Exhibit the Real Zipf's Law-Like Rank Distribution," PLoS ONE, 5(3), 2010 e9411. doi:10.1371/journal.pone.0009411.
[2] W. Li, "Random Texts Exhibit Zipf's-Law-Like Word Frequency Distribution," IEEE Transactions on Information Theory, 38(6), 1992 pp. 1842–1845. doi:10.1109/18.165464.
Permanent Citation
"Zipf's Law for Natural and Random Texts"
http://demonstrations.wolfram.com/ZipfsLawForNaturalAndRandomTexts/
Wolfram Demonstrations Project
Published: September 21 2016