A Random Meeting

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
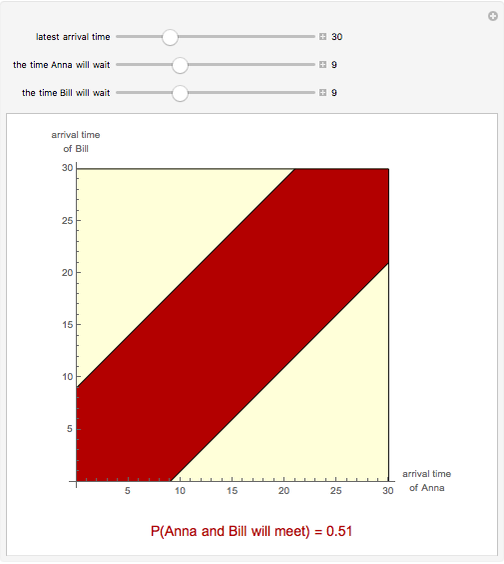
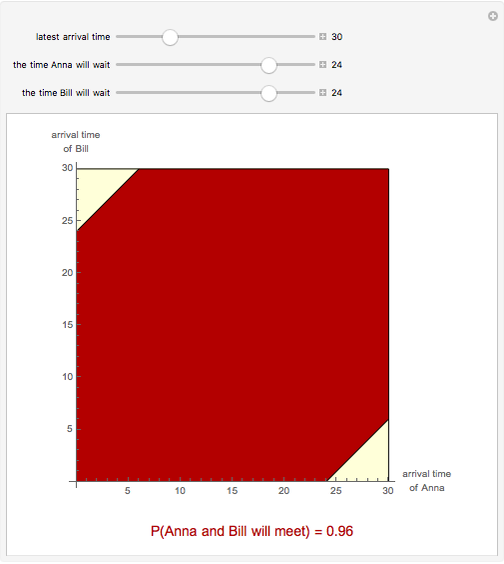
Anna and Bill agree to meet at a certain place in the time interval 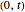 ; time is measured in minutes and the starting time 0 of the interval may be, for example, 11:30. Both arrive at a random moment in the interval
; time is measured in minutes and the starting time 0 of the interval may be, for example, 11:30. Both arrive at a random moment in the interval 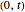 . Moreover, Anna will wait for Bill at most a given number of minutes
. Moreover, Anna will wait for Bill at most a given number of minutes  , and Bill will wait for Anna at most another given number of minutes
, and Bill will wait for Anna at most another given number of minutes  ; both will wait at most until
; both will wait at most until  o’clock. This Demonstration shows the probability that Anna and Bill will meet. The red region in the figure consists of the arrival times of Anna and Bill for which they will meet.
o’clock. This Demonstration shows the probability that Anna and Bill will meet. The red region in the figure consists of the arrival times of Anna and Bill for which they will meet.
Contributed by: Heikki Ruskeepää (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
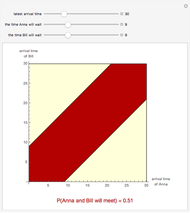
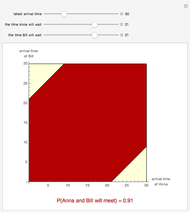
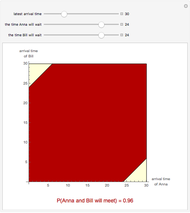
Snapshots 1, 2, and 3: these plots show that if both Anna and Bill wait at most until 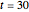 , and they both wait at most 9, 21, or 24 minutes, they will meet with probability 0.51, 0.91, and 0.96, respectively.
, and they both wait at most 9, 21, or 24 minutes, they will meet with probability 0.51, 0.91, and 0.96, respectively.
Let 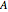 and
and  be the arrival times of Anna and Bill; they are independent and uniformly distributed random variables over the interval
be the arrival times of Anna and Bill; they are independent and uniformly distributed random variables over the interval 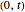 .
.
If 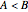 , then Anna arrives first and they meet if
, then Anna arrives first and they meet if 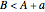 . If
. If 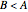 , then Bill arrives first and they meet if
, then Bill arrives first and they meet if 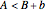 . Thus, they will meet if
. Thus, they will meet if 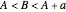 or
or  , in other words, if
, in other words, if 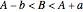 . This is the red region in the figure. The probability that Anna and Bill will meet is, by geometric probability, the area of the red region divided by the area of the square.
. This is the red region in the figure. The probability that Anna and Bill will meet is, by geometric probability, the area of the red region divided by the area of the square.
The Demonstration is based on problem 2 in [1].
Reference
[1] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.
Permanent Citation