Random Harmonic Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
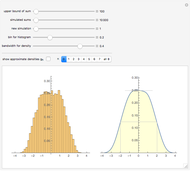
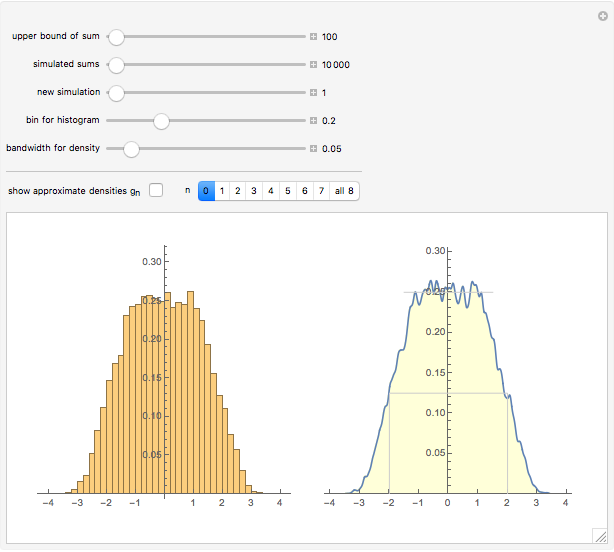
Multiply each term in the harmonic series by a plus or minus sign, which was randomly chosen by flipping a fair coin. The result is a random variable called the random harmonic series. In this Demonstration, we approximate the density of the random harmonic series by simulation. The original infinite sum is replaced by a finite sum, and such a sum is calculated at least ten thousand times. The Demonstration shows a histogram of the values of the sums and a kernel density estimate. The Demonstration can also show a series of special approximate densities (see Details).
Contributed by: Heikki Ruskeepää (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
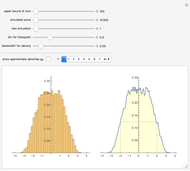
Snapshot 1: too small a bandwidth for the kernel density estimate yields an estimate that varies too much
Snapshot 2: too large a bandwidth for the kernel density estimate yields an estimate that is too smooth
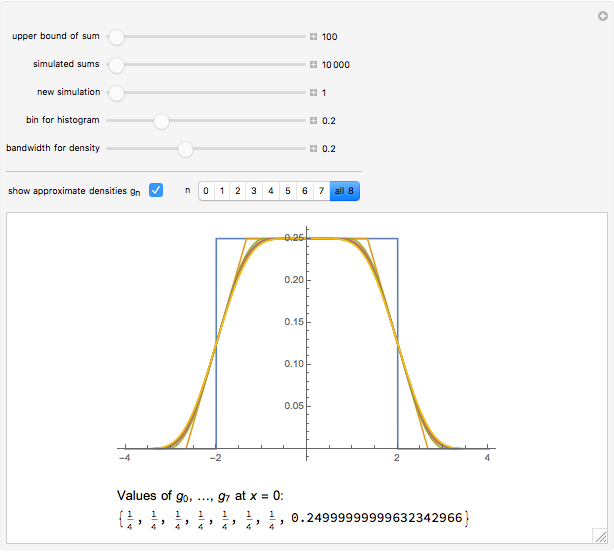
Snapshot 3: This plot shows  for
for 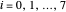 ; see the definition of
; see the definition of 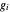 below. As explained there, the functions
below. As explained there, the functions 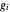 converge to the density of the random harmonic series. We see that, at
converge to the density of the random harmonic series. We see that, at 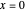 , the approximate densities are all very flat and near to
, the approximate densities are all very flat and near to 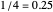 and, at
and, at 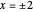 , the approximate densities are all near to
, the approximate densities are all near to 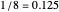 . As explained below, the true values of the density of the random harmonic series at
. As explained below, the true values of the density of the random harmonic series at 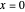 and
and 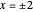 are slightly smaller than
are slightly smaller than 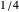 and
and 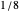 , respectively. Below the plot, we show the values of the approximate densities at
, respectively. Below the plot, we show the values of the approximate densities at 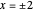 ; thus,
; thus, 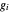 ,
, 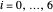 are all
are all 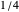 , but
, but 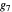 is the first one that is slightly smaller than
is the first one that is slightly smaller than 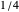 . We also see that there is a very small probability for
. We also see that there is a very small probability for  or
or 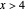 .
.
Recall that the usual harmonic series 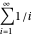 diverges. Following Schmuland [3] (see also Morrison [1] and Nahin [2, pp. 23–24, 229–230]), let
diverges. Following Schmuland [3] (see also Morrison [1] and Nahin [2, pp. 23–24, 229–230]), let 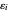 ,
, 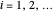 be independent random variables;
be independent random variables; 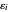 is, for all
is, for all  ,
,  or
or 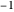 , each with probability
, each with probability 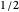 . Consider then the so-called random harmonic series
. Consider then the so-called random harmonic series 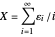 . It can be shown that
. It can be shown that 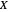 is a continuous random variable and the series converges almost surely. Further, although there is no theoretical upper (or lower) bound on
is a continuous random variable and the series converges almost surely. Further, although there is no theoretical upper (or lower) bound on 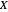 , we have
, we have 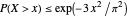 , so that the probability of a very large sum is exceedingly small; for example,
, so that the probability of a very large sum is exceedingly small; for example, 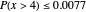 and
and 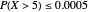 .
.
The density 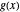 of
of 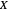 is very flat near the origin, but actually the density does not have a flat top. Although the density is very near to
is very flat near the origin, but actually the density does not have a flat top. Although the density is very near to 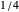 at
at 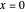 , actually the value is slightly smaller than
, actually the value is slightly smaller than 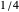 . Also, although the density is very near to
. Also, although the density is very near to  at
at 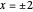 , actually the value is slightly smaller than
, actually the value is slightly smaller than 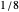 (the exact value is the so-called infinite cosine product integral divided by
(the exact value is the so-called infinite cosine product integral divided by 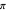 ). In the plot of the estimate of the density of
). In the plot of the estimate of the density of 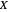 , we have shown a horizontal line at
, we have shown a horizontal line at 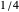 and at
and at 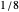 to check how well the estimated density has these theoretical properties
to check how well the estimated density has these theoretical properties .
.
Schmuland defines 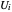 to be a uniform random variable with density
to be a uniform random variable with density  if
if 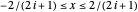 ,
, 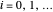 ; these variables are independent. He shows that, almost surely,
; these variables are independent. He shows that, almost surely, 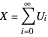 . Let
. Let 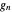 be the density of the partial sum
be the density of the partial sum 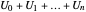 . Then,
. Then, 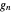 converges to the density
converges to the density 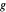 of
of  uniformly on
uniformly on 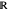 . The density
. The density 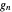 can be calculated either by convolutions or by inverting the characteristic function of the partial sum (which is the product of the characteristic functions of the corresponding
can be calculated either by convolutions or by inverting the characteristic function of the partial sum (which is the product of the characteristic functions of the corresponding 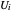 variables). Schmuland shows plots of
variables). Schmuland shows plots of 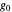 ,
,  , and
, and 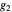 . We have calculated
. We have calculated 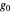 ,
, 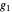 , …,
, …, 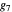 by inverting the characteristic function.
by inverting the characteristic function.
Schmuland shows that  for
for  , but
, but 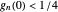 for
for 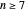 . Indeed, in the Demonstration we calculate that
. Indeed, in the Demonstration we calculate that 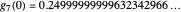 . Schmuland also shows that
. Schmuland also shows that 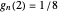 for
for 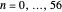 , but
, but  for
for  .
.
References
[1] K. E. Morrison, "Cosine Products, Fourier Transforms, and Random Sums," The American Mathematical Monthly, 102(8), 1995, pp. 716–724.
[2] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton, NJ: Princeton University Press, 2008.
[3] B. Schmuland, "Random Harmonic Series," The American Mathematical Monthly, 110(5), 2003, pp. 407–416.
[4] Wikipedia. "Harmonic Series (Mathematics)." (May 21, 2013) en.wikipedia.org/wiki/Harmonic_series_%28mathematics%29.
Permanent Citation