2D Stokes Flow in a Lid-Driven Cavity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
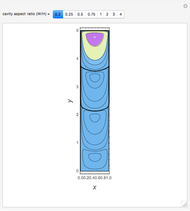
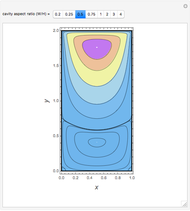
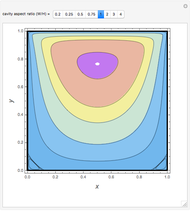
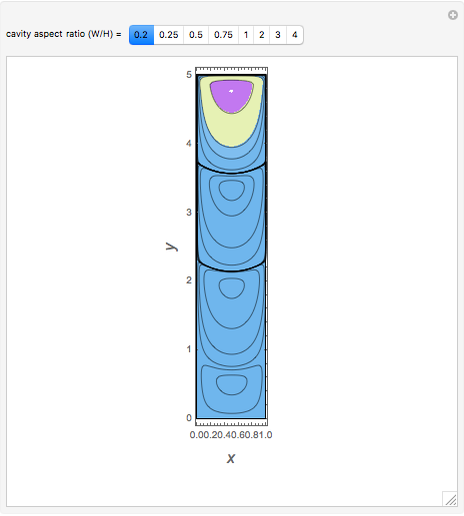
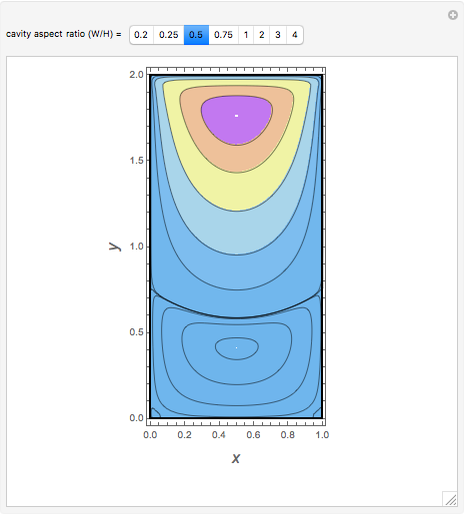
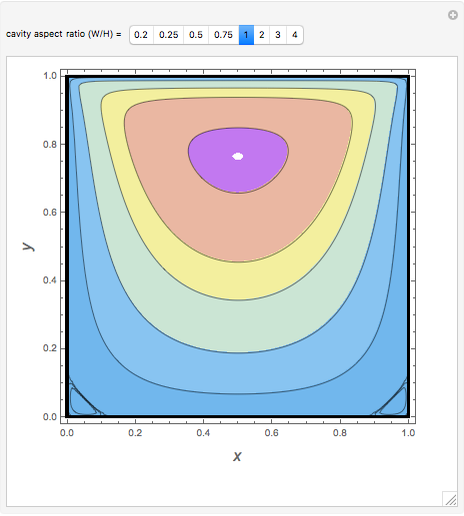
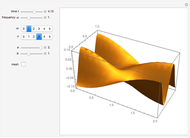
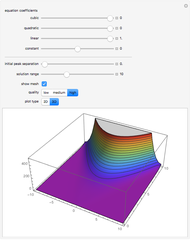
This Demonstration illustrates the steady eddy structure in a 2D driven cavity problem (see [2] and [3]). The stream lines, which at steady state are everywhere tangent to the velocity field, are computed from the stream function ( ) and vorticity (
) and vorticity ( ) formulation for Stokes flow
) formulation for Stokes flow
Contributed by: Brian G. Higgins and Housam Binous (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] H. K. Moffat, "Viscous and Resistive Eddies Near a Sharp Corner," Journal of Fluid Mechanics, 18, 1964 pp. 1–18.
[2] C. Pozrikidis, Introduction to Theoretical and Computational Fluid Dynamics, Oxford: Oxford University Press, 1998.
[3] P. N. Shankar, Slow Viscous Flows, London: Imperial College Press, 2007.
Permanent Citation