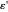3D Stress-Strain Tensor Relations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
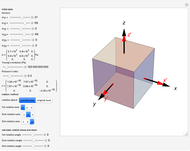
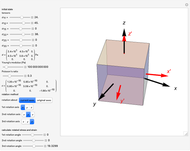
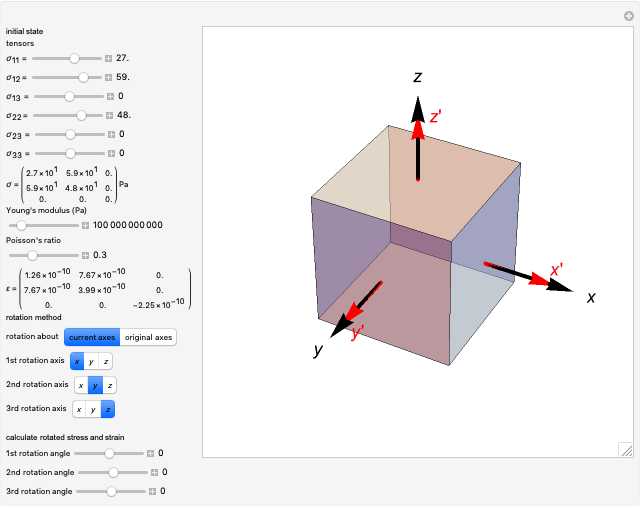
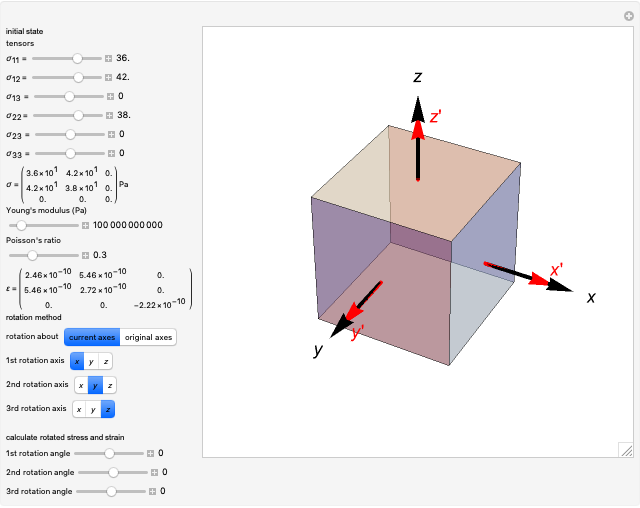
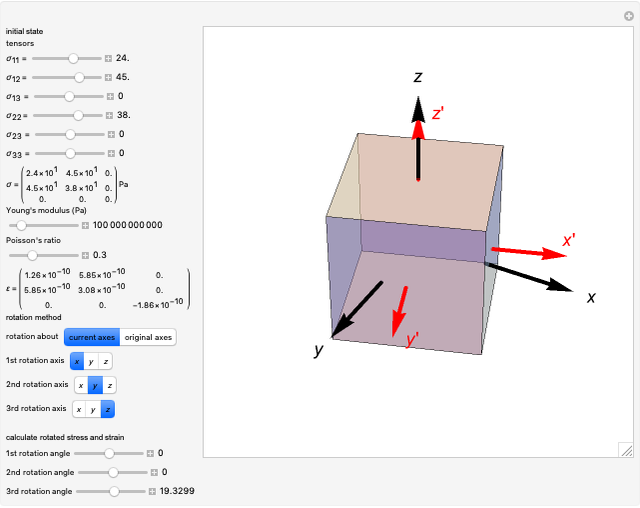
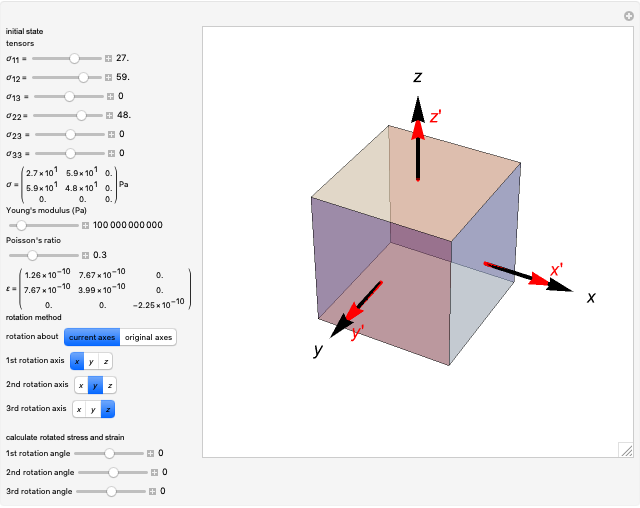
This Demonstration considers stress-strain relationships in the mechanical behavior of materials. Stress is represented by a second-rank tensor 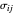 with nine components. However, only six components are independent, since the tensor is symmetrical. We calculate the relationship between uniaxial stress/strain in 3D space. You can select values of Young's modulus
with nine components. However, only six components are independent, since the tensor is symmetrical. We calculate the relationship between uniaxial stress/strain in 3D space. You can select values of Young's modulus 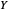 and Poisson's ratio
and Poisson's ratio  , which determine the strain state, represented by the strain tensor
, which determine the strain state, represented by the strain tensor  .
.
Contributed by: Richard Jerue, Leon Tran, Daniel Balerite, Mark Michael, Tanraj Shergill and Joshua Steimel (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] J. P. Steimel. "Materials Science and Engineering." Pacific Open Texts. (May 11, 2022) scholarlycommons.pacific.edu/open-textbooks/8.
[2] Mathematica Stack Exchange. "Resize a Manipulate by Grabbing a Corner." (May 11, 2022) mathematica.stackexchange.com/questions/199234/resize-a-manipulate-by-grabbing-a-corner.
Permanent Citation