A Domain Decomposition Method with Orthogonal Collocation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider the partial differential equation  with
with  and
and  , subject to the boundary and initial conditions
, subject to the boundary and initial conditions  ,
,  , and
, and  . The solution
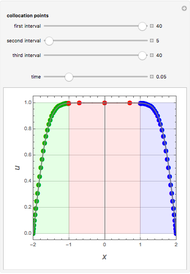
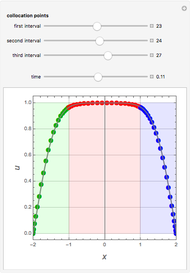
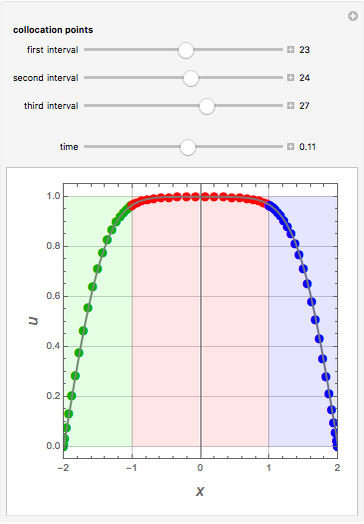
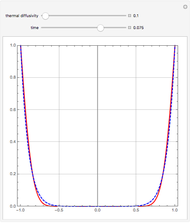
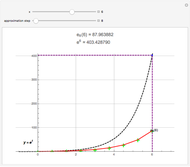
. The solution  is obtained using Mathematica's built-in function NDSolve (solid gray curve) and Chebyshev orthogonal collocation (colored dots). The interval
is obtained using Mathematica's built-in function NDSolve (solid gray curve) and Chebyshev orthogonal collocation (colored dots). The interval  is divided into three regions identified by the green, red, and blue panes. You can vary the number of Chebyshev collocation points in each region independently as well as the time,
is divided into three regions identified by the green, red, and blue panes. You can vary the number of Chebyshev collocation points in each region independently as well as the time,  . The behavior of
. The behavior of 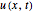 in the different panes dictates how many collocation points one has to choose from. Indeed, for small times the function
in the different panes dictates how many collocation points one has to choose from. Indeed, for small times the function  is almost constant (equal to 1) in the red pane region and varies rapidly in the green and blue panes. This indicates that a small number of collocation points is required in the central region while a large number is required near the edges.
is almost constant (equal to 1) in the red pane region and varies rapidly in the green and blue panes. This indicates that a small number of collocation points is required in the central region while a large number is required near the edges.
Contributed by: Housam Binous (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"A Domain Decomposition Method with Orthogonal Collocation"
http://demonstrations.wolfram.com/ADomainDecompositionMethodWithOrthogonalCollocation/
Wolfram Demonstrations Project
Published: July 8 2013