Picard's Method for Ordinary Differential Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
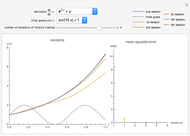
This Demonstration constructs an approximation to the solution to a first-order ordinary differential equation using Picard's method. You can choose the derivative function using the drop-down menu and the initial guess for the algorithm. Increasing the number of iterations displayed using the slider shows closer approximations to the true solution, colored blue in the plot. The mean squared error (MSE) at each iteration is shown on the right.
Contributed by: Oliver K. Ernst (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
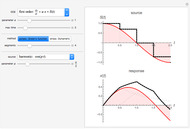
Snapshot 1: the approximations approach the true solution with increasing iterations of Picard's method
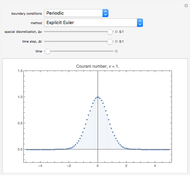
Snapshot 2: the approximation after the first iteration already captures the behavior of the solution
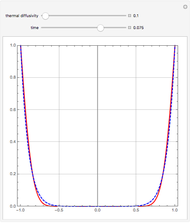
Snapshot 3: although the initial guess is poor, the approximations rapidly improve
Picard's method approximates the solution  to a first-order ordinary differential equation of the form
to a first-order ordinary differential equation of the form
 ,
,
with initial condition  . The solution is
. The solution is
 .
.
Picard's method uses an initial guess  to generate successive approximations to the solution as
to generate successive approximations to the solution as

such that after the  iteration
iteration  .
.
Above, we take  , with
, with  and
and  . Several choices for the initial guess
. Several choices for the initial guess  and differential equation
and differential equation  are possible. After each iteration, the mean squared error of the approximation is computed by sampling the true solution (in blue) and the approximation
are possible. After each iteration, the mean squared error of the approximation is computed by sampling the true solution (in blue) and the approximation  at evenly spaced points in
at evenly spaced points in  .
.
Permanent Citation