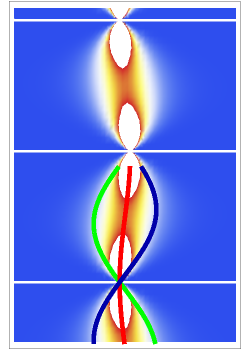
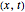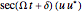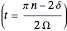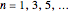A Wave Collapse in the Causal Interpretation of Quantum Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
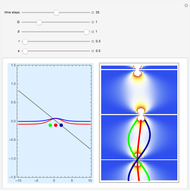
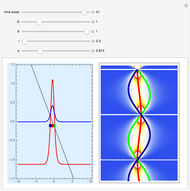
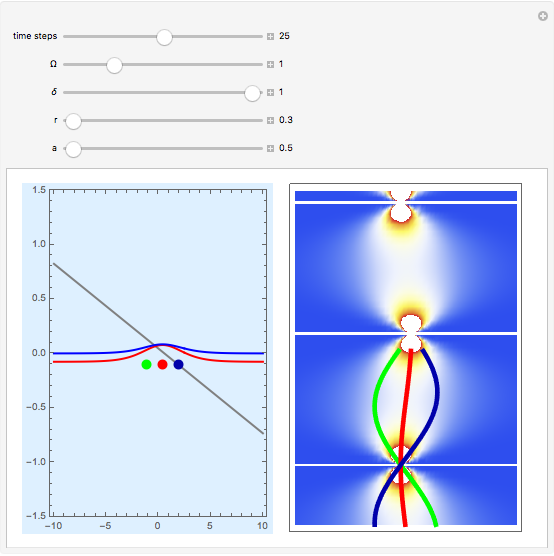
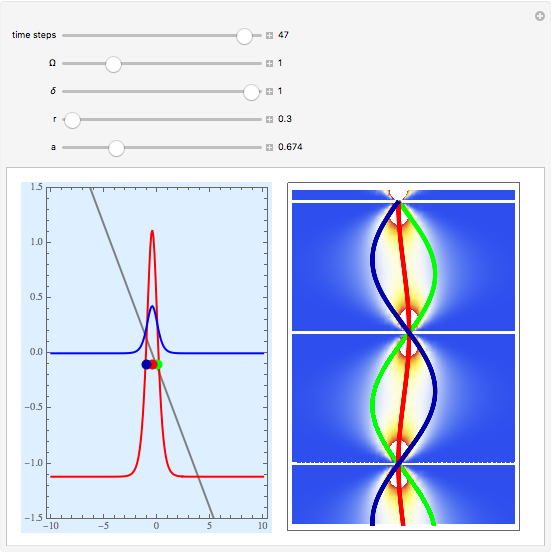
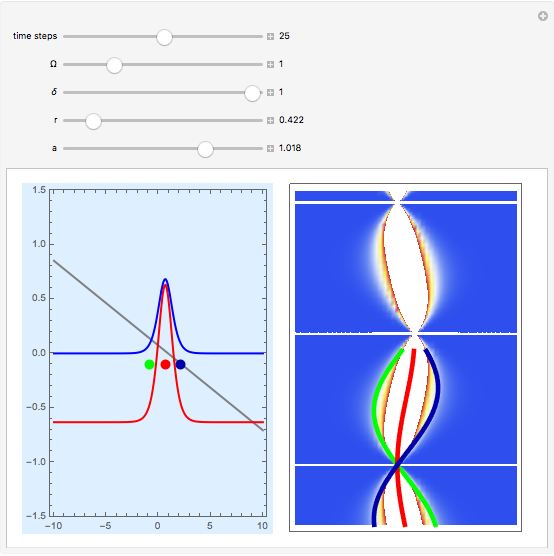
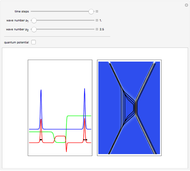
A central consequence of the causal interpretation (CI) is that trajectories do not cross [2, 3]. But what happens to the motion of quantum particles if the wavefunction becomes singular and indefinite? Here, an example is presented for the Gross–Pitaevskii equation with a harmonic potential and a time-dependent nonlinear potential. At certain time steps, where 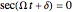 , the squared wavefunction becomes infinitely large and in an infinitesimal region and a singularity occurs.
, the squared wavefunction becomes infinitely large and in an infinitesimal region and a singularity occurs.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Solitons are approximately stable waves that behave as quasi-particles; only for a few cases the equations of motion in the Bohm approach are fully integrable. A notable case is the solitary wave solution of an effective one-dimensional (1D) Bose–Einstein condensate treated by the causal interpretation [1]. The effective Gross–Pitaevskii equation with a harmonic potential, applied here, is:
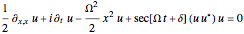 , where
, where 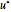 is the complex conjugate,
is the complex conjugate, 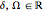 , and
, and 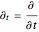 , …. The solitary solution
, …. The solitary solution  can be written:
can be written:

with  .
.
In the eikonal representation of the complex-valued wave  , the gradient of the phase is the particle velocity. This is a linear function with respect to
, the gradient of the phase is the particle velocity. This is a linear function with respect to  , from which the equation of motion is derived by solving:
, from which the equation of motion is derived by solving: 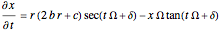 , where the analytic solution is given by
, where the analytic solution is given by 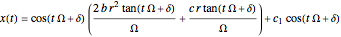 , with the integration constant
, with the integration constant  . The initial positions are distributed linearly around the point
. The initial positions are distributed linearly around the point 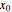 with
with  . It may appear that the presence of the
. It may appear that the presence of the 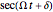 term in the amplitude and in the velocity term of the soliton will lead to singularities at finite times (
term in the amplitude and in the velocity term of the soliton will lead to singularities at finite times (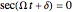 ). The velocity field is multivalued and infinite at these times. With the potential
). The velocity field is multivalued and infinite at these times. With the potential  , the Gross–Pitaevskii equation is the nonlinear analog of the Schrödinger equation.
, the Gross–Pitaevskii equation is the nonlinear analog of the Schrödinger equation.
I am grateful to Detlef Dürr and his collaborator Dustin Lazarovici for helpful suggestions.
References
[1] S. Rajendran, P. Muruganandam, and M. Lakshmanan, "Bright and Dark Solitons in a Quasi 1D Bose–Einstein Condensates Modelled by 1D Gross–Pitaevskii Equation with Time-Dependent Parameters," Physica D, 239, 2010 pp. 366–386 or arXiv:0812.5073[nlin.PS].
[2] P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.
[3] B-G. Englert, M. O. Scully, G. Sussman, and H. Walther, "Surrealistic Bohm Trajectories," Zeitschrift für Naturforschung, 47a, 1992 pp. 1175–1186.
Permanent Citation