The Talbot Carpet in the Causal Interpretation of Quantum Mechanics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
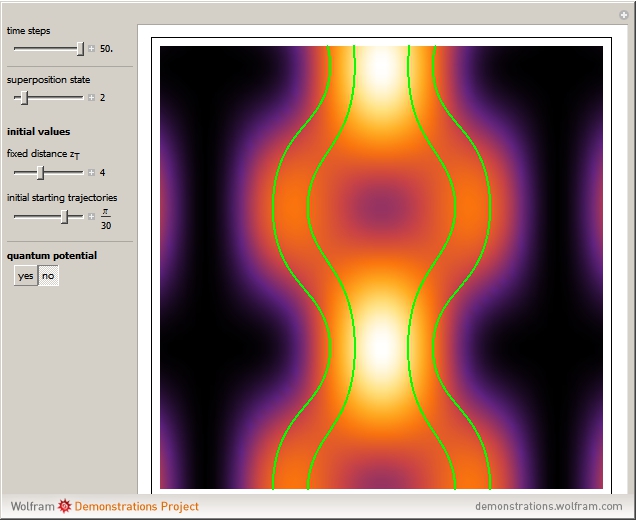
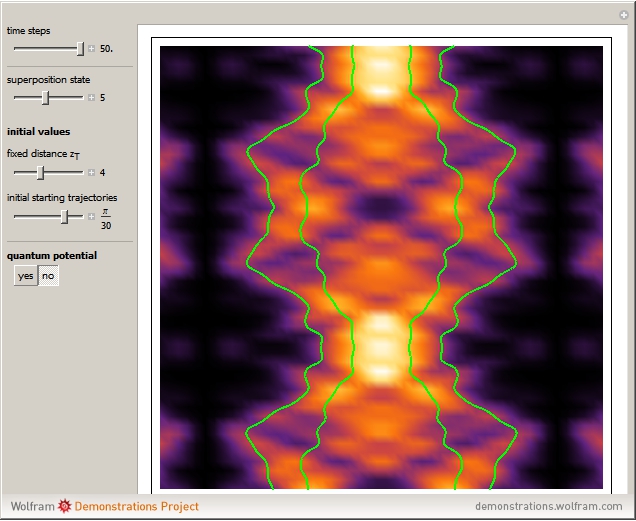
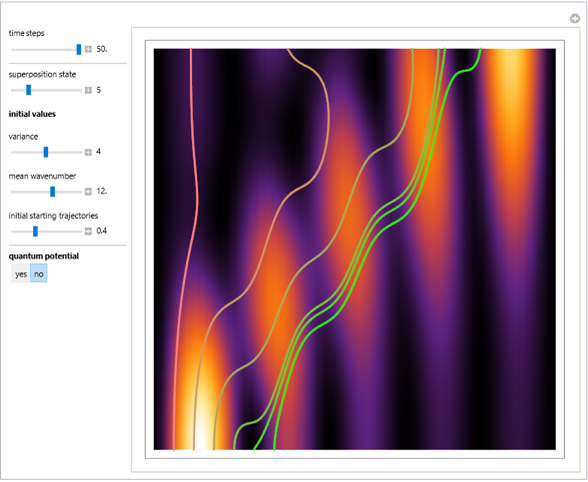
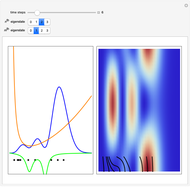
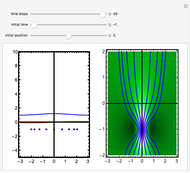
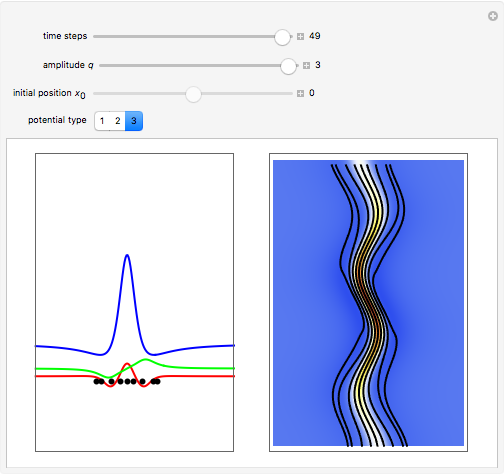
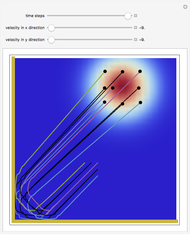
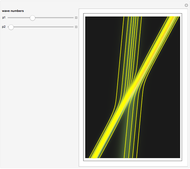
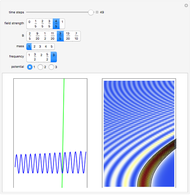
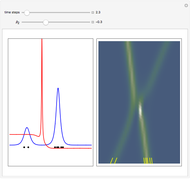
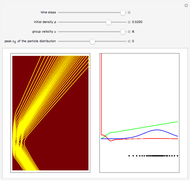
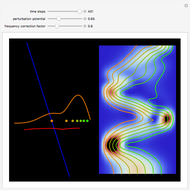
This Demonstration considers a quantum wavepacket containing a superposition of up to 10 stationary states to illustrate the Talbot effect in the causal interpretation of quantum theory. The quantum carpets and the quantum trajectories possess nested fine fractal structure. The wave density is repeated at multiples of a fixed distance  (the Talbot distance).
(the Talbot distance).
Contributed by: Klaus von Bloh (December 2014)
After work by: Enrique Zeleny
Open content licensed under CC BY-NC-SA
Snapshots
Details
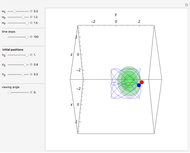
Due to the symmetry of the trajectories and the wavefunction, only half of the trajectories needed to be calculated numerically. The guiding equation for particle velocity from the gradient of the phase of the wavefunction in the energy representation is shown in the related links (Talbot Carpet for a Ronchi Grating and The Superposition Principle in the Causal Interpretation of Quantum Mechanics). In this Demonstration, the phase function  of the
of the  stationary state does not depend on the variable
stationary state does not depend on the variable  . The initial distance between the starting points is 0.05 units of length.
. The initial distance between the starting points is 0.05 units of length.
The quantum carpet wavefunction arises as the solution of the Schrödinger equation:
 , with
, with  ,
,  , and so on.
, and so on.
Local singularities in the velocity  do appear to exist for certain
do appear to exist for certain  and
and  values (nodes where
values (nodes where  ), which make the trajectories unstable.
), which make the trajectories unstable.
To make the results of the program more accurate, increase PlotPoints, AccuracyGoal, PrecisionGoal, and MaxSteps.
References
[1] Bohmian-Mechanics.net. (Dec 22, 2014) www.bohmian-mechanics.net/index.html.
[2] S. Goldstein. "Bohmian Mechanics." Stanford Encyclopedia of Philosophy. (Dec 22, 2014)plato.stanford.edu/entries/qm-bohm.
[3] A. S. Sanz and S. Miret-Artés, "A Causal Look into the Quantum Talbot Effect," The Journal of Chemical Physics, 126(23), 2007 pp. 1–11. doi:10.1063/1.2741555.
Permanent Citation