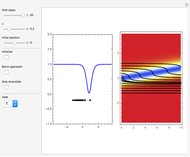
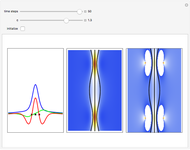
A Breather Solution in the Causal Interpretation of Quantum Mechanics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
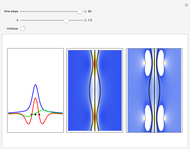
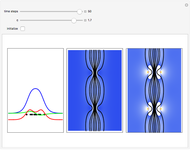
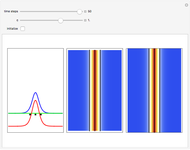
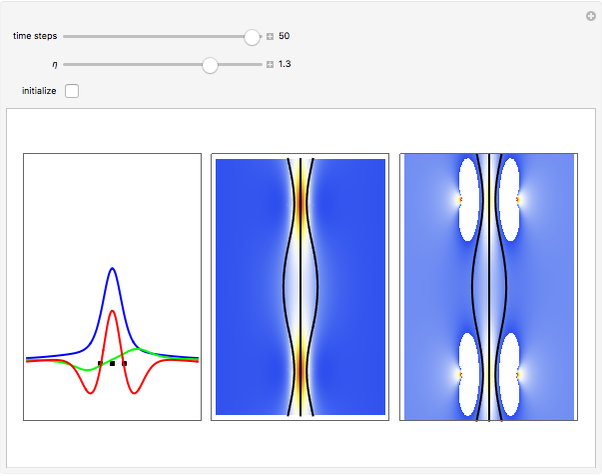
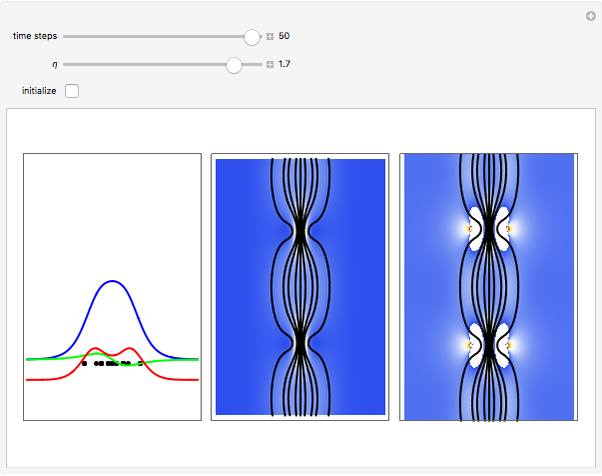
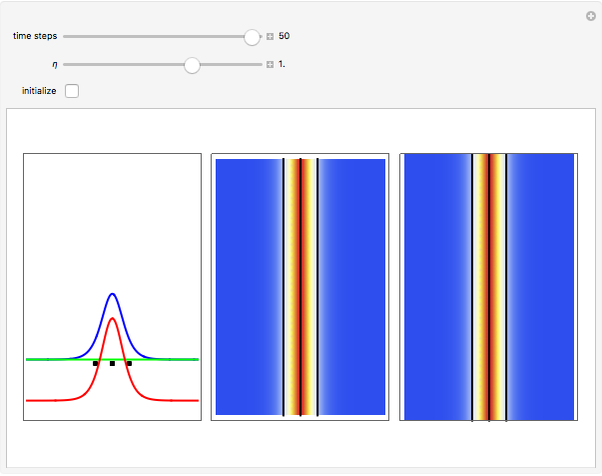
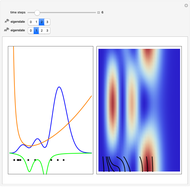
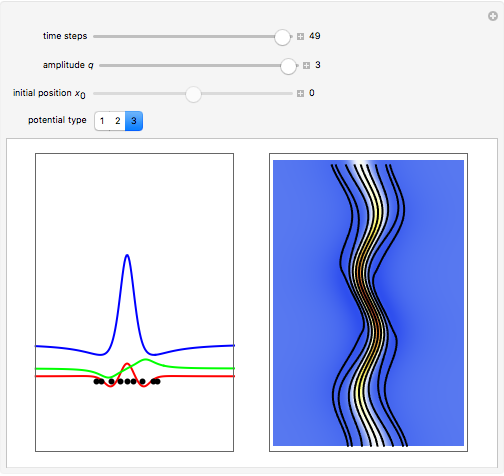
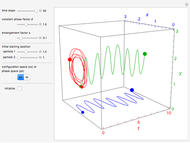
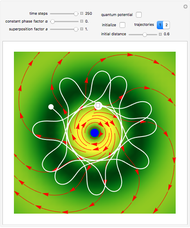
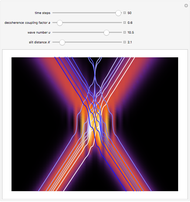
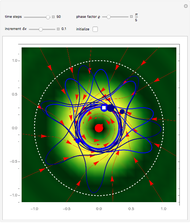
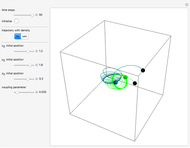
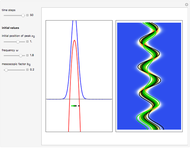
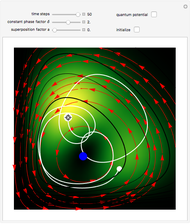
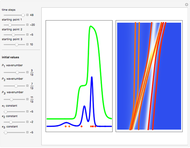
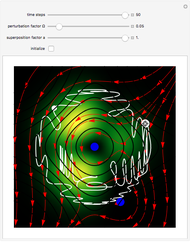
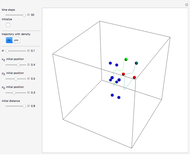
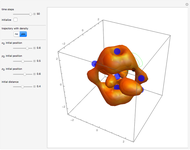
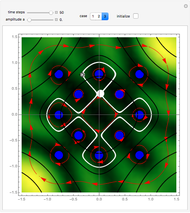
A breather solution appears often in nonlinear wave mechanics, in which a nonlinear wave has energy concentrated in a localized oscillatory manner. This Demonstration studies a breather solution with a hyperbolic secant envelope of the focusing nonlinear Schrödinger (NLS) equation  , with
, with  and so on, also known as the Gross–Pitaevskii equation in the causal interpretation, developed by Louis de Broglie and David Bohm.
and so on, also known as the Gross–Pitaevskii equation in the causal interpretation, developed by Louis de Broglie and David Bohm.
Contributed by: Klaus von Bloh (July 2014)
Open content licensed under CC BY-NC-SA
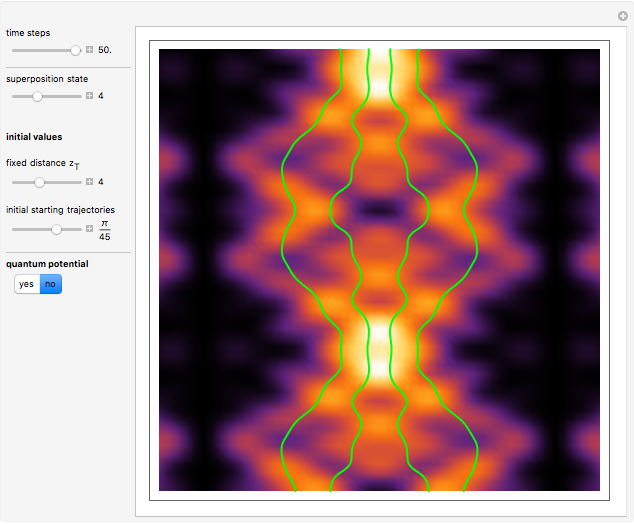
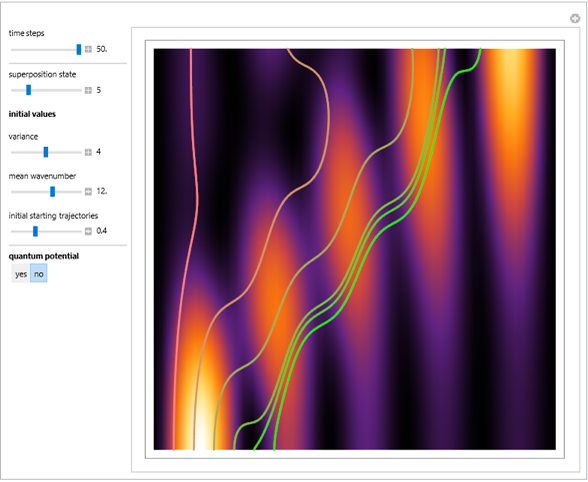
Snapshots
Details
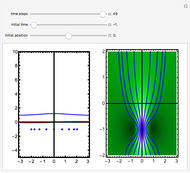
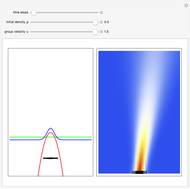
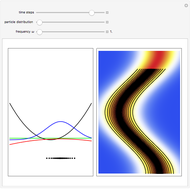
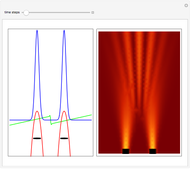
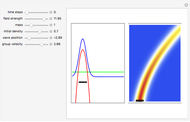
One of the exact breather solutions  for
for  is a complex field as a function of
is a complex field as a function of  and
and  which is periodic in space
which is periodic in space  .
.
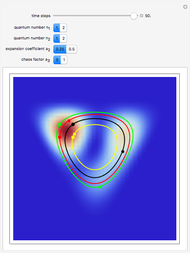
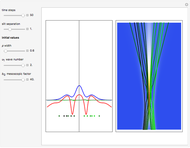
The complex-valued wavefunction
 , with
, with  ,
,
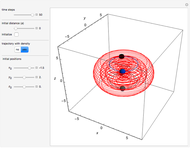
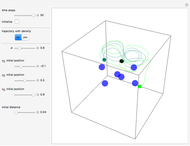
has several remarkable features (see [1]), including periodicity of the squared wavefunction with period  implicit analytic solutions of quantum trajectories for some values
implicit analytic solutions of quantum trajectories for some values  a time-independent solution
a time-independent solution  for
for  and
and  , and a symmetry according to
, and a symmetry according to  , where
, where  , with
, with  . For the case
. For the case  , the wavefunction becomes
, the wavefunction becomes  , where an implicit analytic solution for the quantum motion
, where an implicit analytic solution for the quantum motion  is given by the gradient of the phase function of the wavefunction in the eikonal form (often called polar form). For this special case, the implicit function for
is given by the gradient of the phase function of the wavefunction in the eikonal form (often called polar form). For this special case, the implicit function for  is
is  , with the integration constant
, with the integration constant  .
.
Exploiting to the symmetry of the wave density, only one half of the trajectories were calculated numerically.
On YouTube there are some videos by the author, which show additional breather solutions with a hyperbolic secant envelope in the de Broglie–Bohm interpretation for the Gross–Pitavevskii equation.
[1] D. Schrader, Asymptotisch Auftretende Solitonen-Lösungen der Nichtlinearen Schrödinger-Gleichung zu Beliebigen Secans-Hyperbolicus-Förmigen Anregungen, Aachen, Germany: Shaker Verlag, 1998.
[2] Bohmian-Mechanics.net. (Jul 11, 2014) www.bohmian-mechanics.net/index.html.
[3] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Jul 11, 2014)plato.stanford.edu/entries/qm-bohm.
Permanent Citation