Analytical Solution of Equations for Chemical Transport with Adsorption, Longitudinal Diffusion, Zeroth-Order Production, and First-Order Decay

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
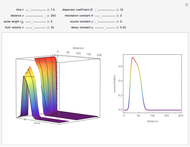
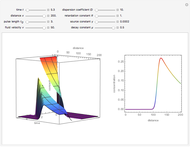
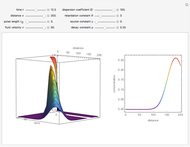
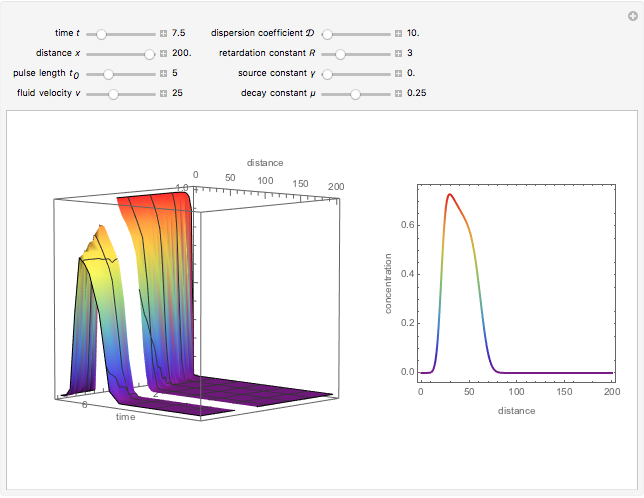
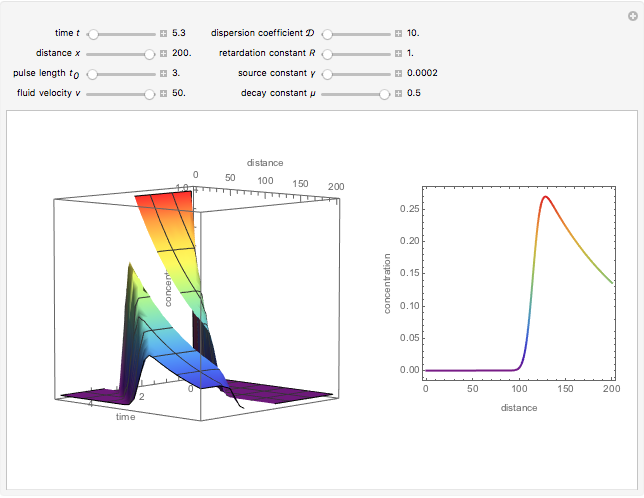
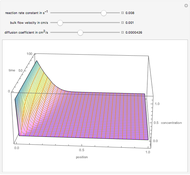
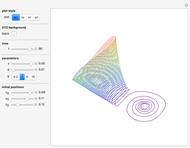
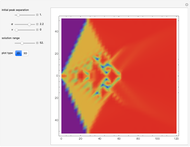
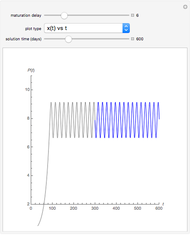
This Demonstration examines one-dimensional chemical transport in a porous medium as influenced by simultaneous adsorption, zeroth-order production, and first-order decay. The corresponding equation is [1]:
[more]
Contributed by: Clay Gruesbeck (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference [1] gives a complete derivation of the analytical solution using Laplace transforms. The solution is:
 ,
,
where
 ,
,
 ,
,
with  .
.
Reference
[1] M. T. Van Genuchten, "Analytical Solutions for Chemical Transport with Simultaneous Adsorption, Zero-Order Production, and First-Order Decay," Journal of Hydrology, 49(3–4), 1981 pp. 213–233. doi:10.1016/0022-1694(81)90214-6.
Permanent Citation