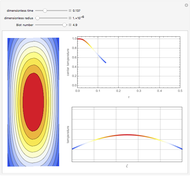
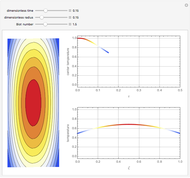
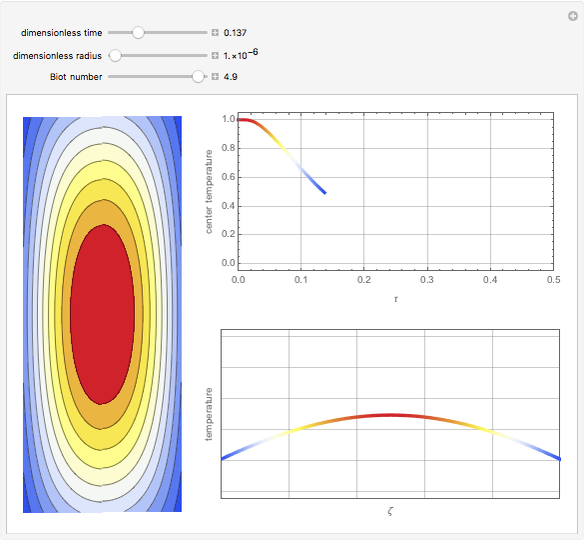
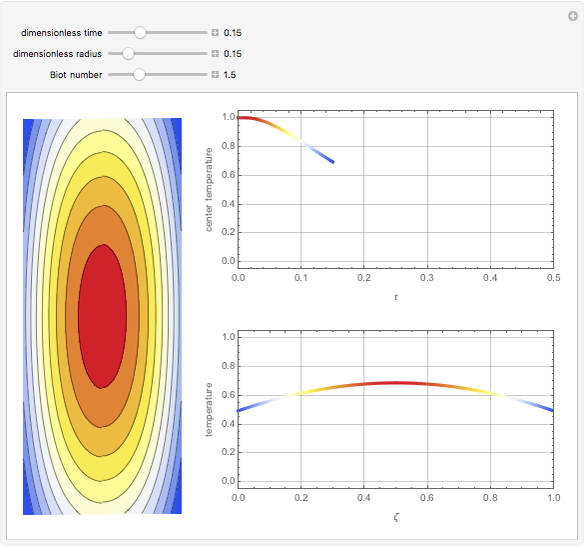
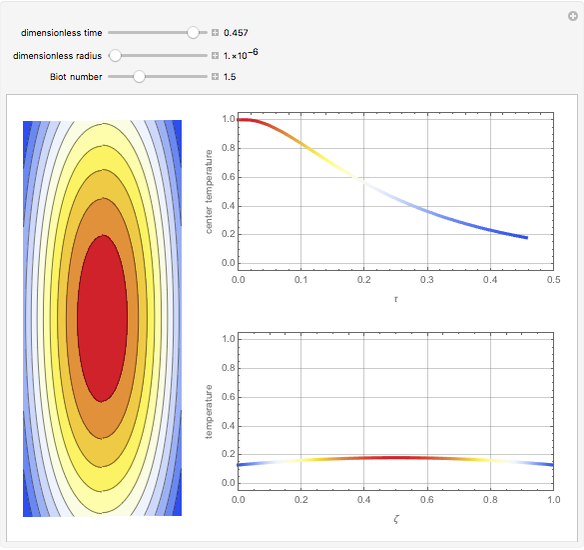
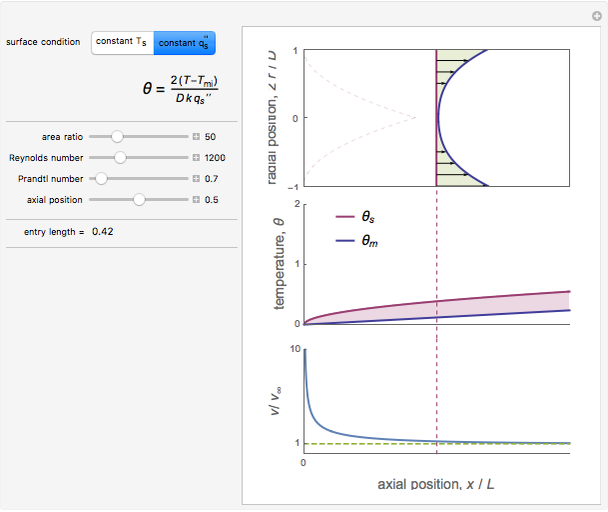
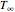This Demonstration simulates the transient cooling of a cylinder that is suddenly immersed in a cooling bath.
Consider a homogeneous solid cylinder of radius  and length
and length  initially at uniform temperature
initially at uniform temperature  . The cylinder is immersed at time
. The cylinder is immersed at time  into a fluid in a well-stirred, insulated tank at constant temperature
into a fluid in a well-stirred, insulated tank at constant temperature 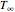 .
.
The equation describing the temperature of the cylinder is:
 ,
,
subject to the following initial and boundary conditions:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
where  is the radial coordinate,
is the radial coordinate,  is the axial coordinate,
is the axial coordinate,  is the thermal diffusivity, and
is the thermal diffusivity, and  is the heat transfer coefficient between the fluid and the cylinder.
is the heat transfer coefficient between the fluid and the cylinder.
This problem is more conveniently solved with the following dimensionless variables:
 : dimensionless temperature,
: dimensionless temperature,
 : dimensionless radial coordinate,
: dimensionless radial coordinate,
 : dimensionless axial coordinate,
: dimensionless axial coordinate,
 : dimensionless time.
: dimensionless time.
The heat equation in terms of these dimensionless variables is:
 ,
,
with
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
where  is the Biot number, the ratio of internal resistance to conductive heat transfer in the cylinder to the external resistance of convective heat transfer of the cylinder to the surrounding fluid. The dimensionless partial differential equation is solved using the built-in Mathematica function NDSolveValue with Neumann boundary conditions for several values of dimensionless time, radius and Biot number.
is the Biot number, the ratio of internal resistance to conductive heat transfer in the cylinder to the external resistance of convective heat transfer of the cylinder to the surrounding fluid. The dimensionless partial differential equation is solved using the built-in Mathematica function NDSolveValue with Neumann boundary conditions for several values of dimensionless time, radius and Biot number.
[less]