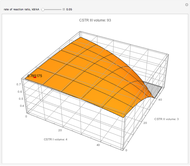
Controlled Release of a Drug from a Hemispherical Matrix
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
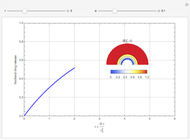
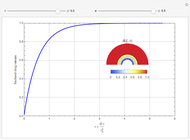
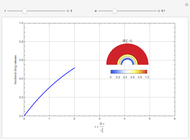
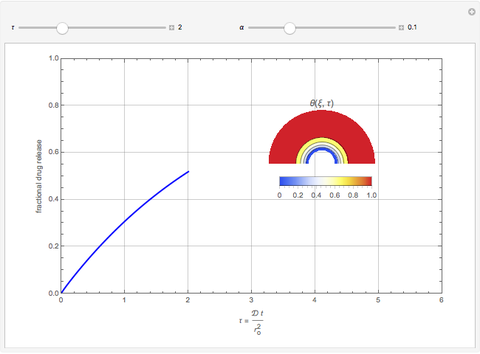
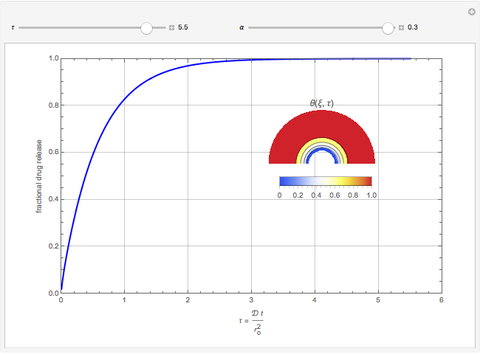
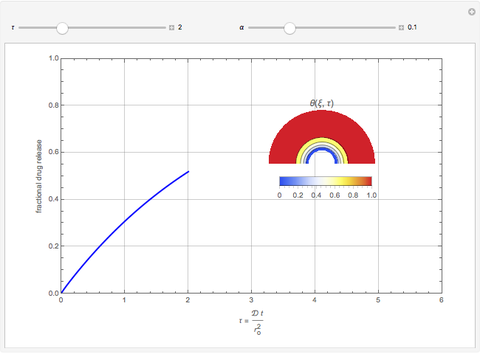
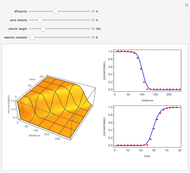
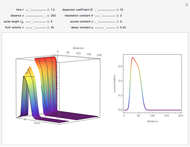
This Demonstration models the release of a drug from a hemispherical matrix.
[more]
Contributed by: Clay Gruesbeck (November 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] R. A. Siegel, "Theoretical Analysis of Inward Hemispheric Release above and below Drug Solubility," Journal of Controlled Release, 69(1), 2000 pp. 109–126. doi:10.1016/S0168-3659(00)00292-3.
Permanent Citation