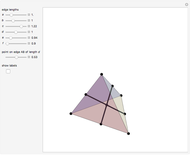
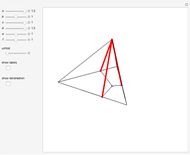
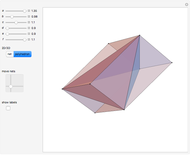
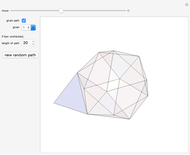
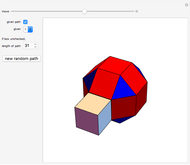
Tetrahedral Loops

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
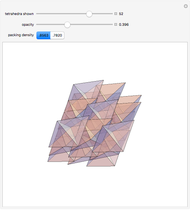
It is not possible to make a chain of regular tetrahedra that meet face to face and have the final one meeting up exactly with the first one. But one can come close.
[more]
Contributed by: Michael Elgersma (Minneapolis) and Stan Wagon (Macalester College) (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
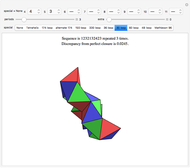
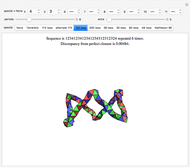
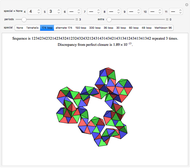
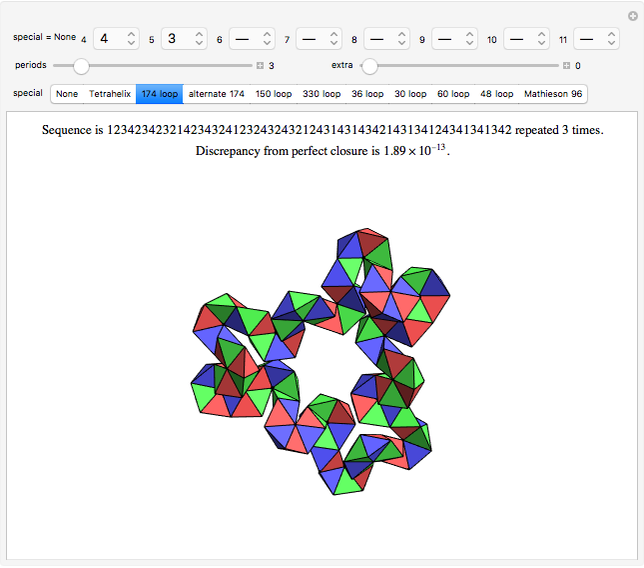
A Steinhaus chain is a sequence of regular tetrahedra such that consecutive ones meet face to face. In 1958 Świerczkowski proved that such a chain cannot end in a tetrahedron that is equal to the first one; the key point of the proof is that the group generated by the four face reflections is a free product of four copies of  . But one can search for chains that approximate a perfect loop and this Demonstration shows several particular chains that have a small gap at the end. These were all found by the authors, except for the 96-loop, due to Robert Mathieson. The controls also allow for exploring various sequences of length 11. The tetrahelix, also called the Boerdijk–Coxeter helix or the Bernal spiral, is a noteworthy spiral of tetrahedra and arises from the sequence 12341234… . The fact that there are loops that come very close to closing up perfectly is evidence for the following conjecture.
. But one can search for chains that approximate a perfect loop and this Demonstration shows several particular chains that have a small gap at the end. These were all found by the authors, except for the 96-loop, due to Robert Mathieson. The controls also allow for exploring various sequences of length 11. The tetrahelix, also called the Boerdijk–Coxeter helix or the Bernal spiral, is a noteworthy spiral of tetrahedra and arises from the sequence 12341234… . The fact that there are loops that come very close to closing up perfectly is evidence for the following conjecture.
Conjecture. For every  there is a Steinhaus chain that has no self-intersections and is within ϵ of closing up perfectly.
there is a Steinhaus chain that has no self-intersections and is within ϵ of closing up perfectly.
References
[1] S. Wagon, Closing a Platonic Gap, The Mathematical Intelligencer, to appear.
[2] S. Wagon, The Banach–Tarski Paradox, New York: Cambridge University Press, 1985.
Permanent Citation