Binary Diffusion Coefficients for Gases

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
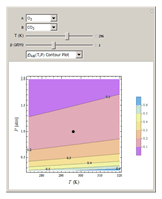
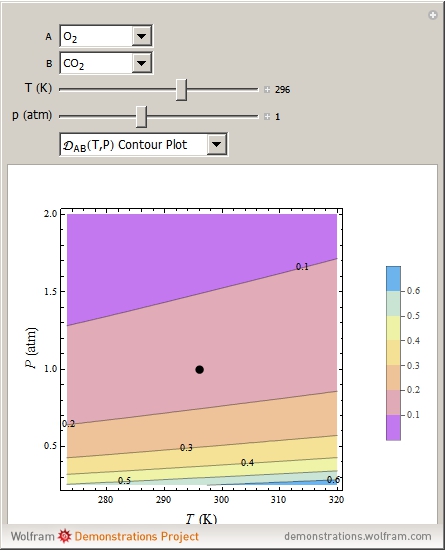
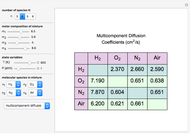
Binary diffusion coefficients  at low to moderate pressures (such that the ideal gas behavior is valid) can be predicted with reasonable accuracy (to within about 5% of experimental data) from the kinetic theory of gases using results from the Chapman–Enskog theory based on the Lennard–Jones (6-12) potential [1].
at low to moderate pressures (such that the ideal gas behavior is valid) can be predicted with reasonable accuracy (to within about 5% of experimental data) from the kinetic theory of gases using results from the Chapman–Enskog theory based on the Lennard–Jones (6-12) potential [1].
Contributed by: Brian G. Higgins and Housam Binous (February 2013)
Open content licensed under CC BY-NC-SA
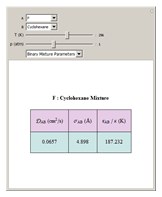
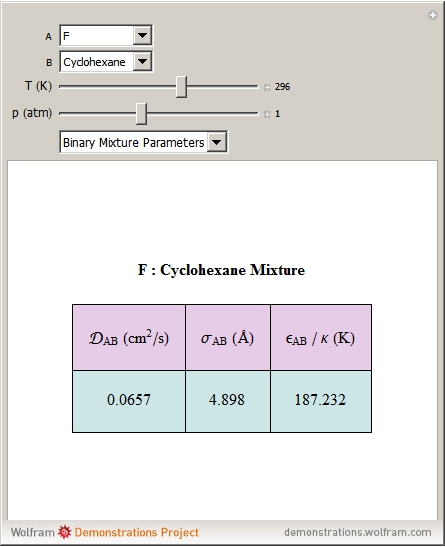
Snapshots
Details
A brief outline of the formulas used in the calculations is given below. The calculations are based on the Lennard–Jones (6-12) potential:
 .
.
In the above expression,  is called the collision diameter (a measure of the diameter of the molecule), and
is called the collision diameter (a measure of the diameter of the molecule), and  is the maximum energy of attraction between a pair of molecules. The resulting working equation from Chapman–Enskog kinetic theory for estimating the product of the mixture molar density with binary diffusion coefficient
is the maximum energy of attraction between a pair of molecules. The resulting working equation from Chapman–Enskog kinetic theory for estimating the product of the mixture molar density with binary diffusion coefficient  is
is
 ,
,
where  is the molar density of the binary mixture,
is the molar density of the binary mixture,  (g/mol) is the molecular weight of species
(g/mol) is the molecular weight of species  , and
, and  is the binary collision diameter, which is estimated from collision diameter parameters
is the binary collision diameter, which is estimated from collision diameter parameters  using the following mixing rule:
using the following mixing rule:
 .
.
The quantity  is called the collision integral for diffusion and is a function of the reduced temperature
is called the collision integral for diffusion and is a function of the reduced temperature  , defined as
, defined as
 .
.
In this expression,  is the Boltzmann constant and
is the Boltzmann constant and  is the characteristic energy appearing in the Lennard–Jones potential for the binary pair estimated using the mixing rule
is the characteristic energy appearing in the Lennard–Jones potential for the binary pair estimated using the mixing rule
 ,
,
where the units of  are kelvins. For ideal gases, we can estimate
are kelvins. For ideal gases, we can estimate  as
as  . The resulting binary diffusivity is then given by
. The resulting binary diffusivity is then given by
 ,
,
where  is in atm. In these calculations, a correlation for
is in atm. In these calculations, a correlation for  as a function of the reduced temperature
as a function of the reduced temperature  is computed from data (table E.2 in [1]). The molecular parameters for the individual species are taken from table E.1 in [1].
is computed from data (table E.2 in [1]). The molecular parameters for the individual species are taken from table E.1 in [1].
Reference
[1] R. B. Bird, W. E. Stewart, and E. N. Lightfoot, Transport Phenomena, 2nd ed., New York: John Wiley & Sons, 2002.
Permanent Citation