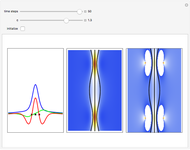
Causal Interpretation for an Electron Passing through Two Narrow Slits
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
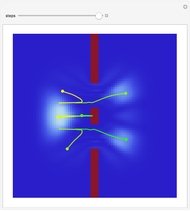
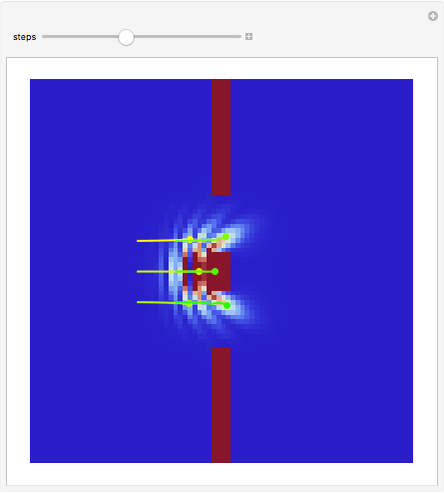
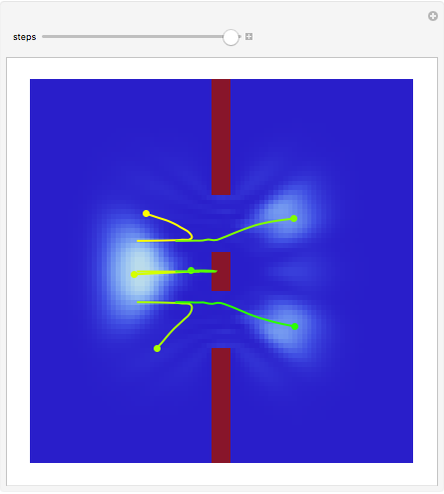
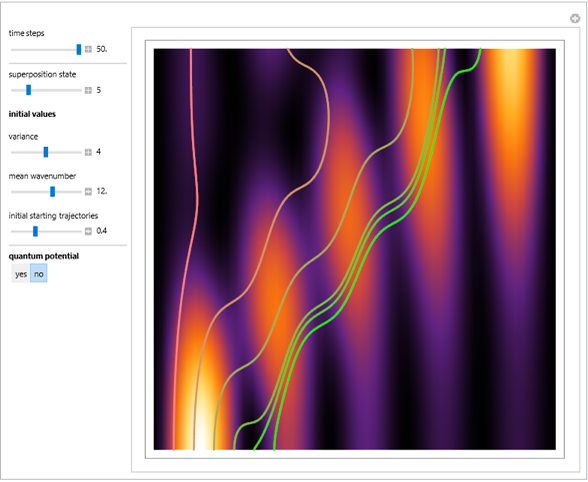
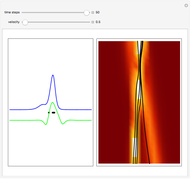
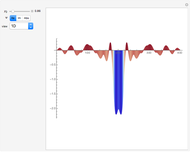
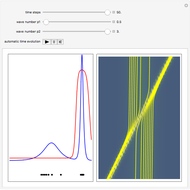
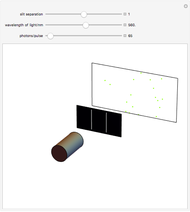
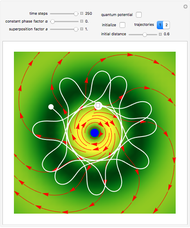
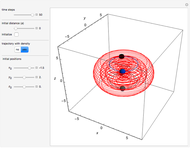
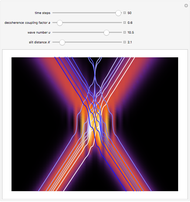
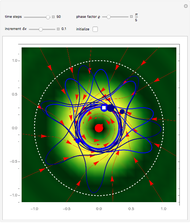
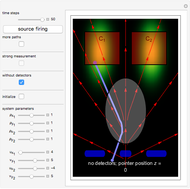
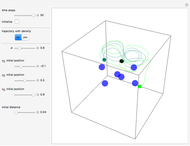
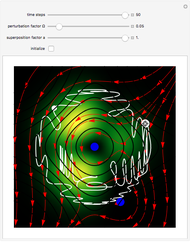
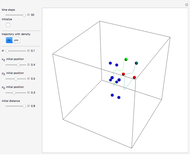
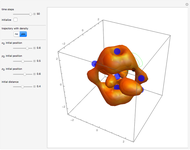
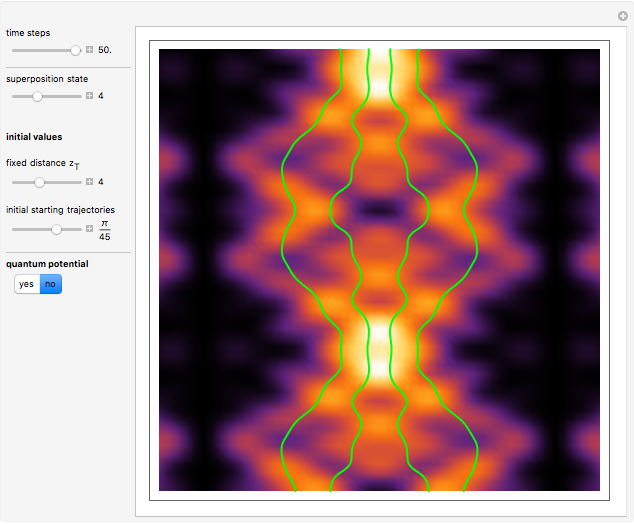
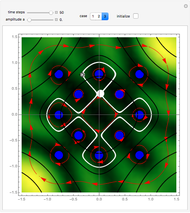
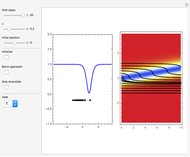
This Demonstration covers the same process described inProbability Density for an Electron Passing through Two Narrow Slits, but with an extension to the causal interpretation of quantum theory developed by L. de Broglie and D. Bohm. With the numerical technique, you can see fine details of the scattering process both near and far from the narrow slits.
Contributed by: Klaus von Bloh (August 2012)
Based on a program by: Enrique Zeleny and Paul Nylander
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information see [1], [2], and [3]. The numerical method to calculate the velocity from a discrete function is, in general, not very stable, but the applied interpolation function leads to an accurate approximation of the physical event; due to the numerical errors produced by the limited mesh of 80 mesh points, the velocity term must be adjusted (here using 5/8 instead of 1).
References
[1] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Aug 6, 2012) plato.stanford.edu/entries/qm-bohm.
[2] Wikipedia. "Crank–Nicolson Method." (Aug 6, 2012) en.wikipedia.org/wiki/Crank-Nicolson_method.
[3] I. Galbraith, Y. S. Ching, and E. Abraham, "Two-Dimensional Time-Dependent Quantum-Mechanical Scattering Event," American Journal of Physics, 52(1), 1984 pp. 60–68. doi: 10.1119/1.13811.
Probability Density for an Electron Passing through Two Narrow Slits
Enrique Zeleny
The Superposition Principle in the Causal Interpretation of Quantum Mechanics
Klaus von Bloh
Two-Soliton Collision for the Gross-Pitaevskii Equation in the Causal Interpretation
Klaus von Bloh
One-Slit Diffraction Pattern
Enrique Zeleny
Soliton Trajectories of the Modified Korteweg-de Vries Equation (mKdV)
Klaus von Bloh
Scattering by a Square-Well Potential
M. Hanson
Dressed Multi-Particle Electron Wave Functions
Michael Trott with permission of Springer
Bohm Trajectories
Michael Trott
Double Slit Diffraction for Particles
Katelyn Rogers
Wave-Particle Duality in the Double-Slit Experiment
S. M. Blinder
-
Bohm Trajectories for the Two-Dimensional Coulomb Potential
Klaus von Bloh -
Bohm Trajectories in an LCAO Approximation for the Hydrogen Molecule H_2
Klaus von Bloh -
Decoherence and Trajectories Implied by a Modified Schrodinger Equation
Klaus von Bloh -
Bohm Trajectories for a Particle in a Two-Dimensional Circular Billiard
Klaus von Bloh -
From Bohm to Classical Trajectories in a Hydrogen Atom
Klaus von Bloh -
Continuous Transition between Quantum and Classical Behavior for a Harmonic Oscillator
Klaus von Bloh -
Continuous Transition between Classical and Bohm Quantum Pictures for Young's Interference Experiment
Klaus von Bloh -
Bohm Trajectories for Quantum Particles in a Uniform Gravitational Field
Klaus von Bloh -
Bohm Trajectories for a Particle in a Two-Dimensional Calogero-Moser Potential
Klaus von Bloh -
Nonlocality in the de Broglie-Bohm Interpretation of Quantum Mechanics
Klaus von Bloh -
Three-Soliton Collision in the Trajectory Approach
Klaus von Bloh -
The Which-Way Experiment and the Conditional Wavefunction
Klaus von Bloh -
Chaotic Quantum Motion of Two Particles in a 3D Harmonic Oscillator Potential
Klaus von Bloh -
Perturbation Theory in the de Broglie-Bohm Interpretation of Quantum Mechanics
Klaus von Bloh -
Periodic Quantum Motion of Two Particles in a 3D Harmonic Oscillator Potential
Klaus von Bloh -
Quantum Motion of Two Particles in a 3D Trigonometric Pöschl-Teller Potential
Klaus von Bloh -
The Talbot Carpet in the Causal Interpretation of Quantum Mechanics
Klaus von Bloh -
Bohmian Quantum Trajectories for Coherent States of the Pöschl-Teller Potential
Klaus von Bloh -
Gray and Dark Solitons in the de Broglie and Bohm Approaches
Klaus von Bloh -
A Breather Solution in the Causal Interpretation of Quantum Mechanics
Klaus von Bloh