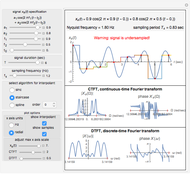
Chebyshev Spectral Differentiation via Fast Fourier Transform

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
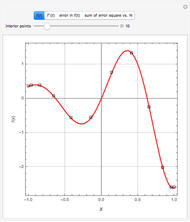
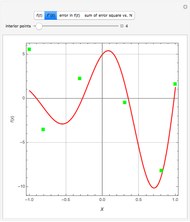
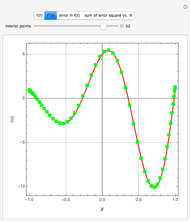
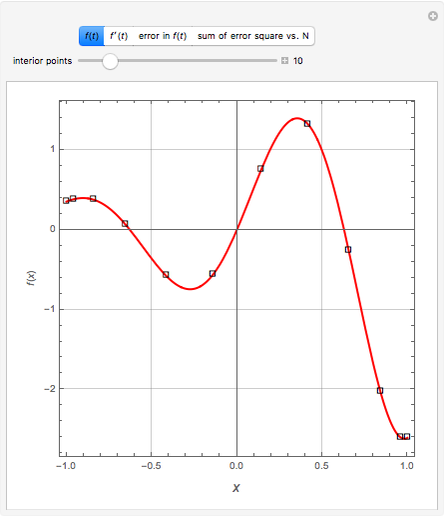
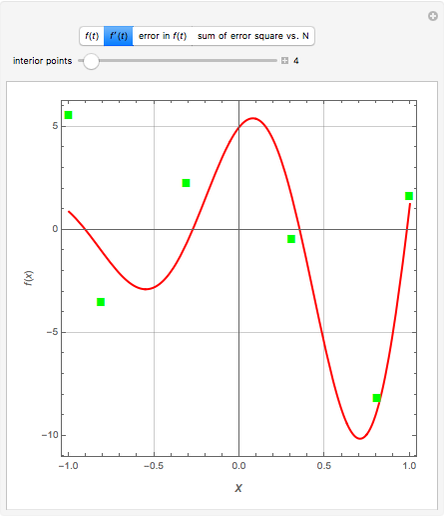
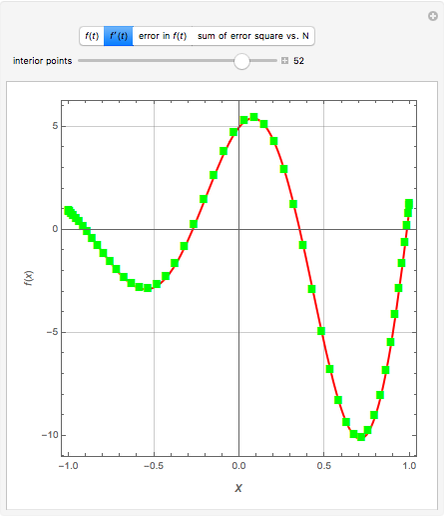
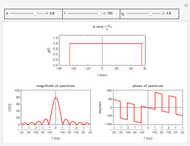
Consider the function 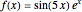 with derivative
with derivative 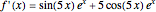 . This Demonstration uses Chebyshev differentiation via Fast Fourier Transform (FFT) [1] to estimate
. This Demonstration uses Chebyshev differentiation via Fast Fourier Transform (FFT) [1] to estimate 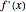 at the
at the 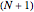 Chebyshev–Gauss–Lobatto points. You can change the number of interior points,
Chebyshev–Gauss–Lobatto points. You can change the number of interior points, 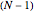 . The error (i.e., the difference between the exact and approximate values of
. The error (i.e., the difference between the exact and approximate values of 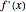 ) decreases for large values of
) decreases for large values of  .
.
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (March 2013)
Open content licensed under CC BY-NC-SA
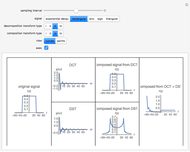
Snapshots
Details
Here are the steps for Chebyshev differentiation via the fast Fourier transform (FFT) [1] algorithm:
1. Take the Chebyshev–Gauss–Lobatto points given by 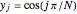 with
with 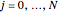 . These points are the extrema of the Chebyshev polynomial of the first kind,
. These points are the extrema of the Chebyshev polynomial of the first kind,  .
.
2. Calculate  and form the vector
and form the vector 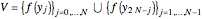 .
.
3. Calculate 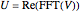 , the real part of the
, the real part of the 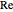 and
and 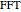 of
of 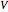 .
.
4. Compute 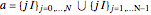 , where
, where  ; then calculate
; then calculate 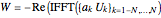 where
where 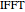 is the inverse fast Fourier transform.
is the inverse fast Fourier transform.
5. Use the vector  to evaluate
to evaluate 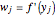 (i.e., the approximate derivative calculated at the Chebyshev–Gauss–Lobatto points) for
(i.e., the approximate derivative calculated at the Chebyshev–Gauss–Lobatto points) for 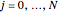 :
:
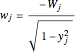 for
for 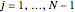 ,
,
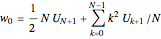 ,
,
and 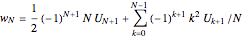 .
.
Reference
[1] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.
Permanent Citation