Kuramoto Model for Phase Locking of Coupled Oscillators

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
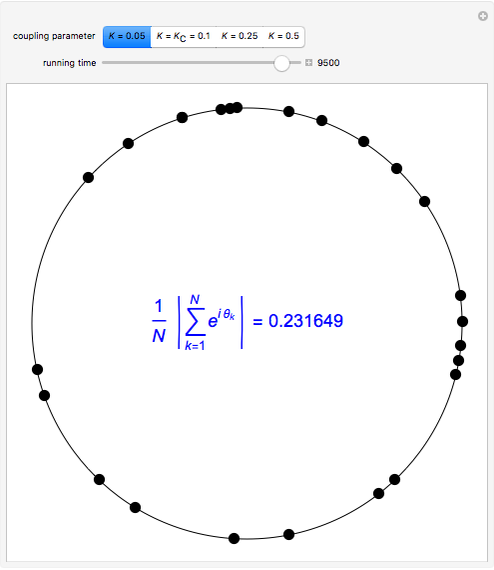
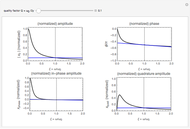
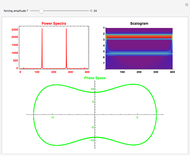
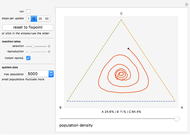
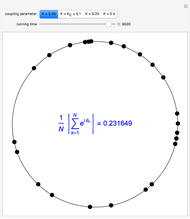
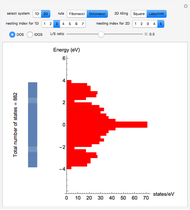
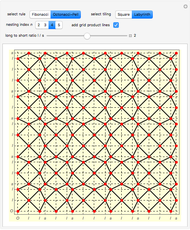
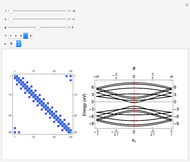
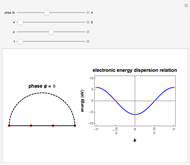
This Demonstration shows the collective synchronization of  coupled oscillators according to the Kuramoto model [1], which is a modified version of the Winfree model [2] for the population of biological oscillators.
coupled oscillators according to the Kuramoto model [1], which is a modified version of the Winfree model [2] for the population of biological oscillators.
Contributed by: Jessica Alfonsi (September 2016)
Padova, Italy
Open content licensed under CC BY-NC-SA
Snapshots
Details
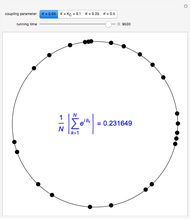
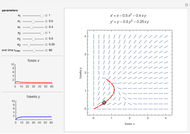
Snapshot 1: weak coupling parameter  , incoherent behavior
, incoherent behavior
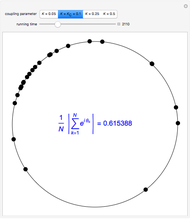
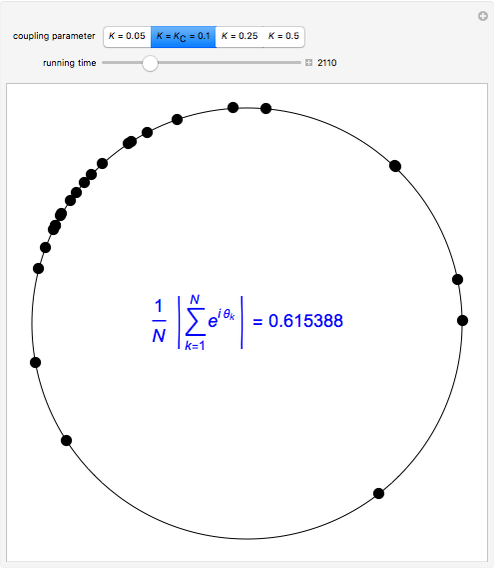
Snapshot 2: critical coupling parameter  , onset of partial synchronization, but incoherent behavior is still present
, onset of partial synchronization, but incoherent behavior is still present
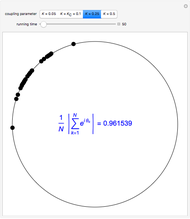
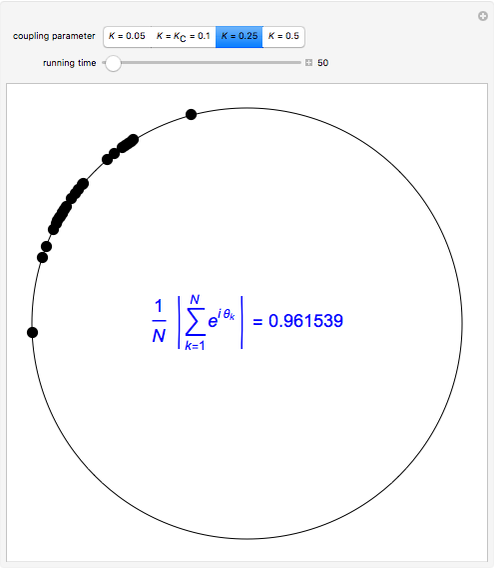
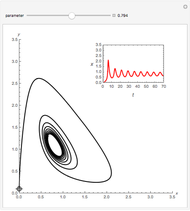
Snapshot 3: strong coupling parameter  , synchronization reached after a short transient, order parameter close to 1
, synchronization reached after a short transient, order parameter close to 1
References
[1] Y. Kuramoto, Chemical Oscillations, Waves and Turbulence, Berlin: Springer-Verlag, 1984.
[2] A. T. Winfree, The Geometry of Biological Time, New York: Springer-Verlag, 1980.
[3] S. H. Strogatz, "From Kuramoto to Crawford: Exploring the Onset of Synchronization in Populations of Coupled Oscillators," Physica D: Nonlinear Phenomena, 143(1–4), 2000 pp. 1–20. doi:10.1016/s0167-2789(00)00094-4.
[4] J. A. Acebrón, L. L. Bonilla, C. J. Pérez Vicente, F. Ritort and R. Spigler, "The Kuramoto Model: A Simple Paradigm for Synchronization Phenomena," Reviews of Modern Physics, 77(1), 2005 pp. 137–185. doi:10.1103/RevModPhys.77.137.
Permanent Citation