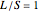Electronic Structure of 1D and 2D Quasiperiodic Systems

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
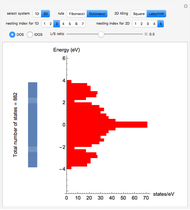
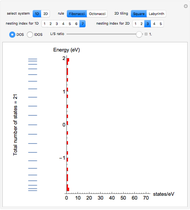
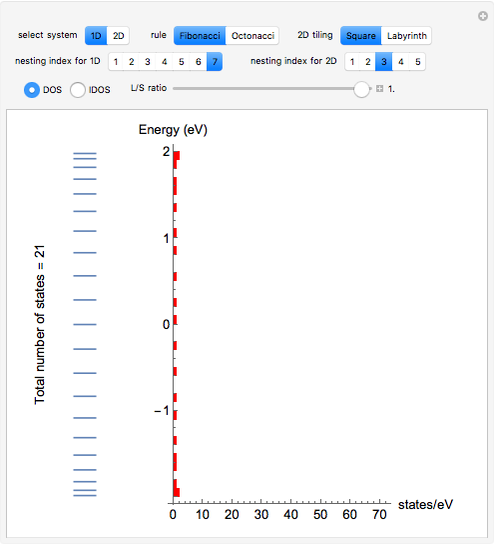
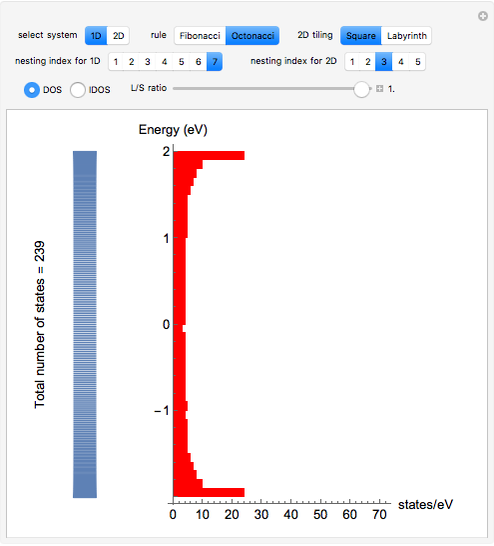
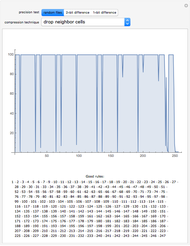
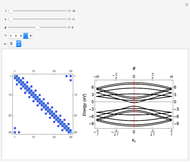
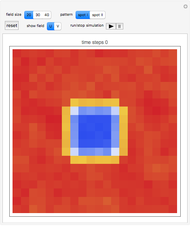
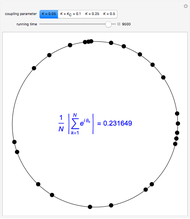
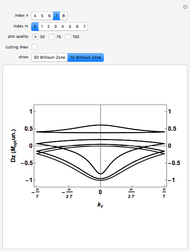
This Demonstration shows the electronic levels of 1D and 2D aperiodic systems compared with the related electronic density of states (DOS) and integrated DOS (IDOS). The latter are computed as histograms, counting the number of electronic levels in a given energy bin. The electronic structure is calculated using the tight-binding method [1].
[more]
Contributed by: Jessica Alfonsi (July 2013)
(Padova, Italy)
Open content licensed under CC BY-NC-SA
Details
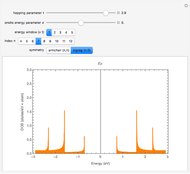
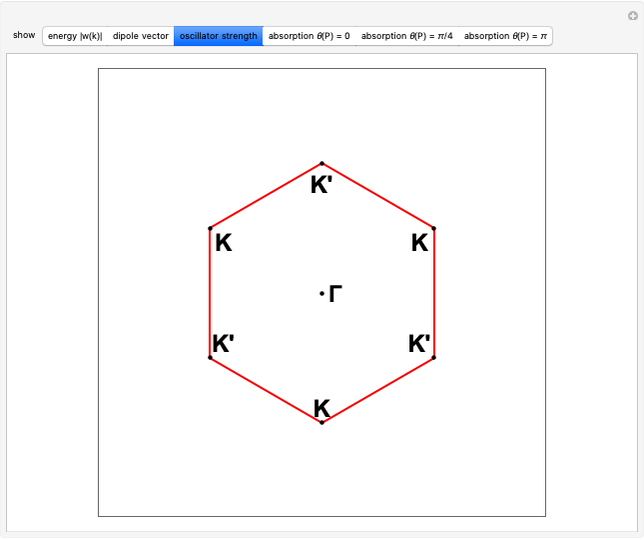
Snapshot 1: electronic density of states for the 1D Fibonacci system with periodic order (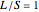 )
)
Snapshot 2: electronic density of states for the 1D octonacci system with periodic order (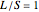 )
)
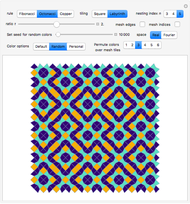
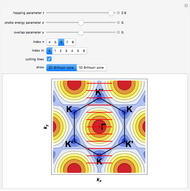
Snapshot 3: electronic density of states for the 2D Fibonacci system (square tiling) with aperiodic order ( )
)
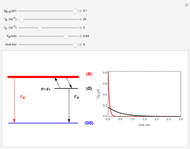
Snapshot 4: integrated electronic density of states for the 1D Fibonacci system with periodic order (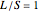 )
)
Snapshot 5: integrated electronic density of states for the 1D octonacci system with periodic order (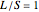 )
)
Snapshot 6: integrated electronic density of states for the 2D Fibonacci system (square tiling) with aperiodic order ( )
)
Reference
[1] U. Grimm and M. Schreiber, "Energy Spectra and Eigenstates of Quasiperiodic Tight-Binding Hamiltonians," in Quasicrystals: Structure and Physical Properties (H.-R. Trebin, ed.), Weinheim, Germany: Wiley-VCH, 2003 pp. 210–235. arxiv.org/abs/cond-mat/0212140.
Snapshots
Permanent Citation