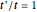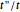Models for Edge States in the Electronic Spectra of Dimer Chains

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
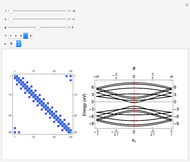
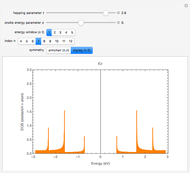
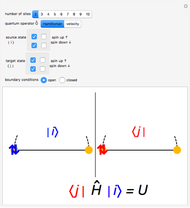
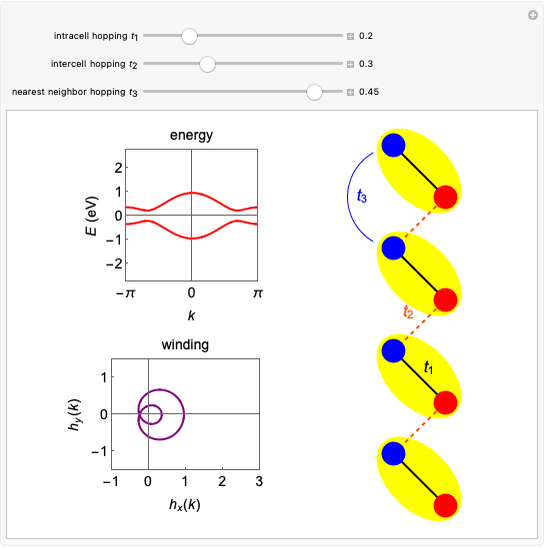
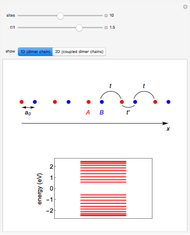
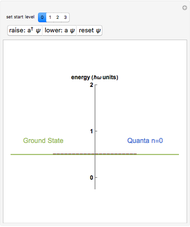
This Demonstration shows two simple toy models for the appearance of zero-energy states in a one-dimensional (1D) system such as a simple finite chain of dimers and a two-dimensional (2D) system built from coupled finite chains of dimers. The electronic Hamiltonian matrix is solved in both cases within the tight-binding formalism, where  is the hopping matrix element between
is the hopping matrix element between 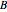 -type and
-type and 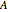 -type sites, whereas
-type sites, whereas 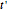 is the hopping matrix element between
is the hopping matrix element between 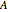 -type and
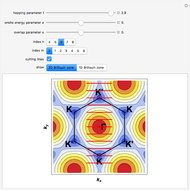
-type and 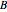 -type sites within each finite chain. In the 2D case, the inter-chain coupling parameter
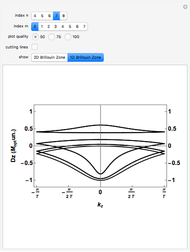
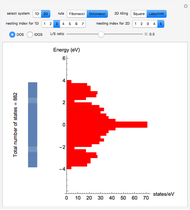
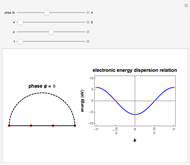
-type sites within each finite chain. In the 2D case, the inter-chain coupling parameter 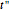 affects the dispersivity of the electronic bands: if
affects the dispersivity of the electronic bands: if 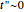 , the bands are almost flat. It was shown in [1] that tuning the ratio
, the bands are almost flat. It was shown in [1] that tuning the ratio 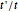 introduces anisotropy into the system, therefore inducing a topological transition governing the localization properties at the system edges. Hence, if
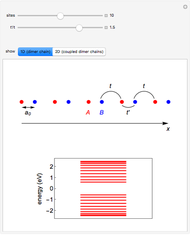
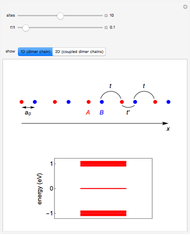
introduces anisotropy into the system, therefore inducing a topological transition governing the localization properties at the system edges. Hence, if 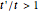 , there will be no zero energy states, whereas if
, there will be no zero energy states, whereas if 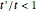 , edge states appear in the electronic spectra. [2] rationalizes this topological transition in terms of a geometrical phase, the so-called Zak phase, which is equal to
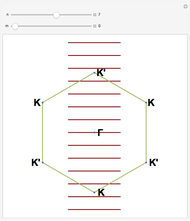
, edge states appear in the electronic spectra. [2] rationalizes this topological transition in terms of a geometrical phase, the so-called Zak phase, which is equal to  in the presence of edge states; otherwise it is zero. The Zak phase is related to another relevant geometric phase (the Berry phase) by contour integration over the first Brillouin zone (see [1] and references therein).
in the presence of edge states; otherwise it is zero. The Zak phase is related to another relevant geometric phase (the Berry phase) by contour integration over the first Brillouin zone (see [1] and references therein).
Contributed by: Jessica Alfonsi (September 2014)
(Padova, Italy)
Open content licensed under CC BY-NC-SA
Snapshots
Details
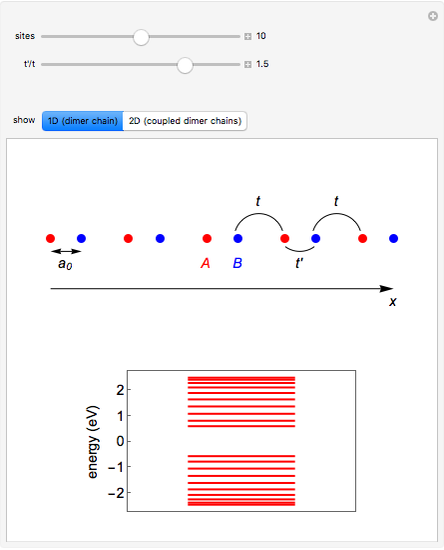
Snapshot 1: absence of edge states in a chain of dimers 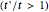
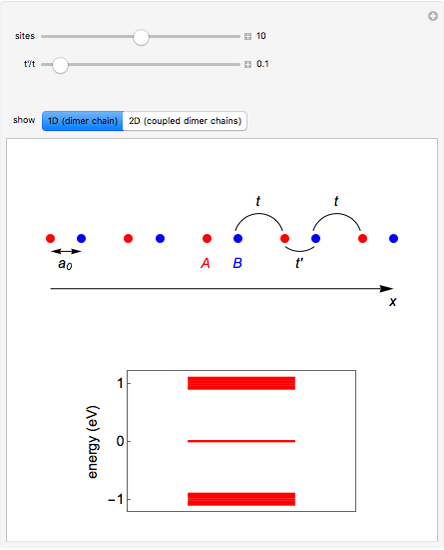
Snapshot 2: appearance of edge states in a chain of dimers 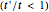
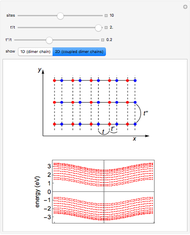
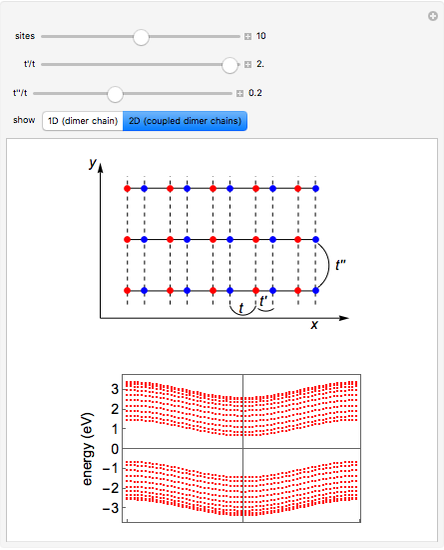
Snapshot 3: absence of edge states in a 2D system made of coupled chains of dimers 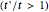
Snapshot 4: turning point of the topological transition for the onset of edge states in a 2D system made of coupled chains of dimers 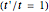
Snapshot 5: edge states in a 2D system made of coupled chains of dimers 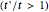 and enhanced dispersion of energy bands
and enhanced dispersion of energy bands 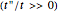
References
[1] P. Delplace, "États de bord et cônes de Dirac dans des cristaux bidimensionnels," Ph.D. thesis, Université Paris-Sud XI, France, 2010. tel.archives-ouvertes.fr/tel-00607781/fr.
[2] P. Delplace, D. Ullmo, and G. Montambaux, "Zak Phase and the Existence of Edge States in Graphene," Physical Review B, 84(19), 2011 pp. 195452–195464. journals.aps.org/prb/abstract/10.1103/PhysRevB.84.195452.
Permanent Citation