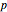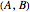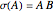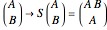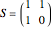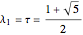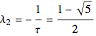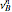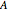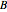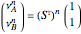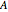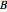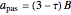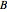Spectral Properties of 1D Fibonacci Quasicrystals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
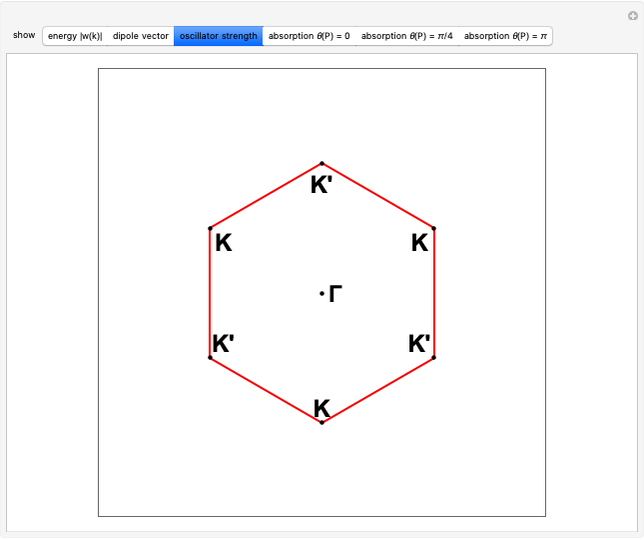
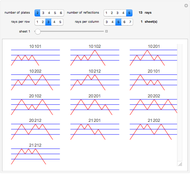
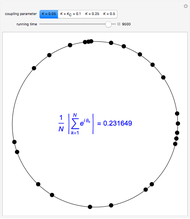
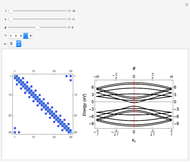
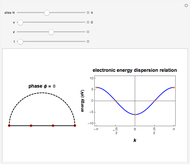
This Demonstration shows the spectral properties of the Fibonacci quasicrystal from both algebraic and graphical points of view; in the latter case in real and reciprocal space. The Fibonacci quasicrystal is the most studied one-dimensional (1D) quasiperiodic model structure, given its interesting applications in photonics and acoustics.
[more]
Contributed by: Jessica Alfonsi (November 2018)
(Padova, Italy)
Open content licensed under CC BY-NC-SA
Details
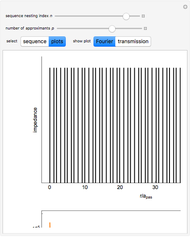
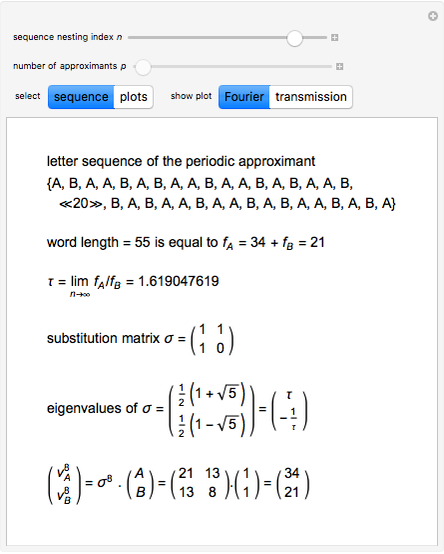
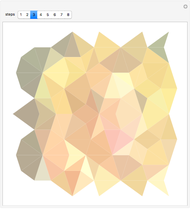
Snapshot 1: letter sequence for the single periodic approximant at the initial stage with 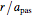 , with a frequency ratio limit still far from the golden number
, with a frequency ratio limit still far from the golden number
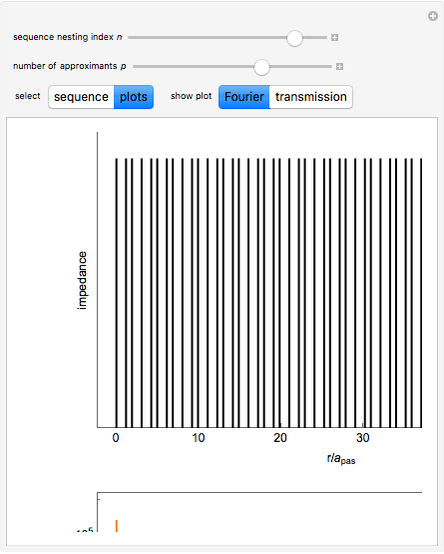
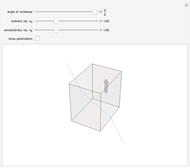
Snapshot 2: same as the Thumbnail image but with transmission plot (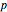 ,
, 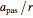 ) enabled, instead of the Fourier power spectrum
) enabled, instead of the Fourier power spectrum
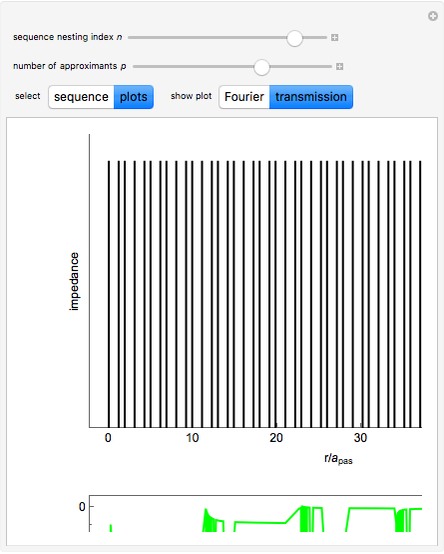
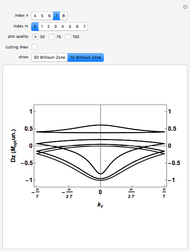
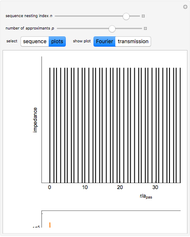
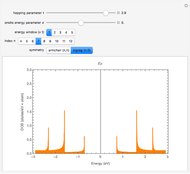
Snapshot 3: Fourier spectrum similar to the Thumbnail image but with a higher  value, therefore with more spectral components
value, therefore with more spectral components
References
[1] W. Steurer and D. Sutter-Widmer, "Photonic and Phononic Quasicrystals," Journal of Physics D: Applied Physics, 40(13), 2007 R229. doi:10.1088/0022-3727/40/13/R01.
[2] U. Grimm and M. Schreiber, "Energy Spectra and Eigenstates of Quasiperiodic Tight-Binding Hamiltonians," Quasicrystals: Structure and Physical Properties (H.-R. Trebin, ed.), Weinheim, Germany: Wiley-VCH, 2003 pp. 210–235. arxiv.org/abs/cond-mat/0212140.
Snapshots
Permanent Citation