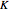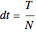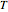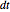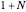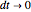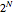Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Convergence of Binomial Option Pricing under Nonconstant Volatility

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

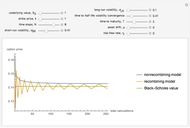
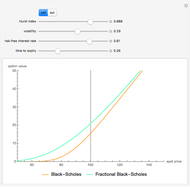
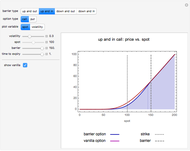
This Demonstration is a continuation and test of the validity of a modeling approach presented by the Wolfram Demonstration European Binomial Option Pricing with Nonconstant Volatility. That Demonstration presents a model for pricing an option using binomial option pricing techniques when volatility of the underlying asset is not deemed to be constant through time.

[more]

An option gives the holder the right but not the obligation to buy an asset (with value ) at some point in the future () for a price agreed upon today (strike price ). Cox, Ross, and Rubinstein [2] were the first to present a simplified approach of valuing this right. They employ a binomial process for the value of the underlying asset. There are discrete changes in the value of the underlying asset that occur over a set length of time (, where is the time until maturity and is the total number of steps in the binomial tree). The sizes of the expected changes (up and down moves in the binomial tree) during each length of time are driven by the volatility of the underlying asset during that length. When this volatility is constant through each , the magnitude of the movements is also constant; therefore, the binomial tree recombines. Once this is completed for all , there will be possible outcomes. By taking the maximum between and for each, and iterating backward through the tree (as in [2]), an estimated value for that option is calculated. As , the expected value from the binomial approach converges to the true value.

When volatility is not constant through time, if is constant, magnitudes of the binomial movements will also not be constant. This makes the binomial tree not recombine, meaning after movements there will be possible outcomes. Guthrie [1] presents an approach where rather than having constant and changing up and down movement magnitudes, there can be constant up and down movements over varying lengths of . This allows the tree to recombine.

To test the model's validity, we can benchmark the value calculated against the Black–Scholes value (the most generally accepted valuation approach for European options [3]). The Demonstration presents the value calculated by each model ( axis) relative to the total number of calculations required after the price process and outcomes have been estimated to calculate it ( axis).

The Demonstration highlights the nonlinearity of the nonrecombining approach regarding the size of computation required to approximate a value. It also strongly supports the use and validity of the model developed by [1].

[less]

Contributed by: Tom Stannard (November 2015)
Open content licensed under CC BY-NC-SA

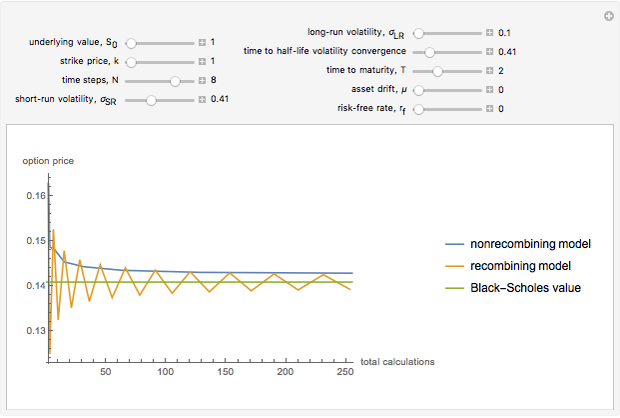
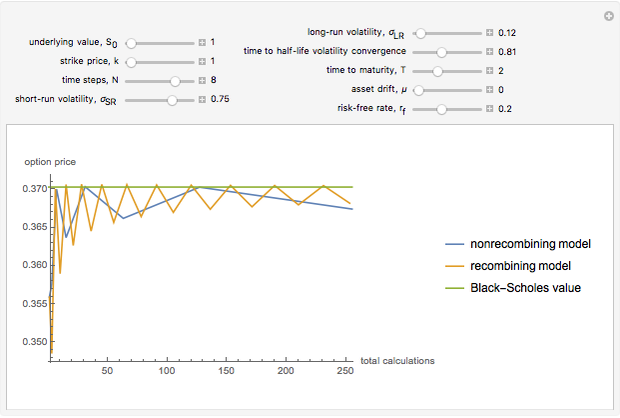
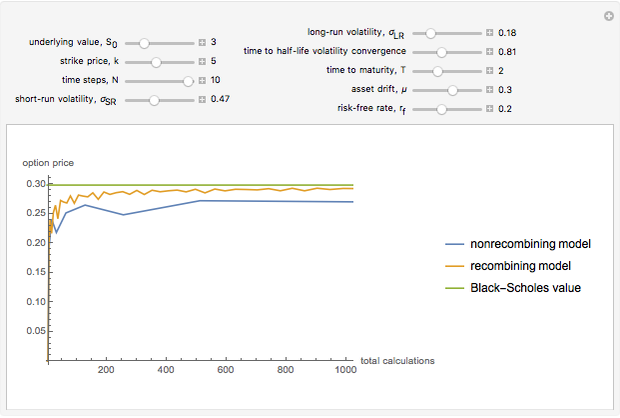
Snapshots

Details

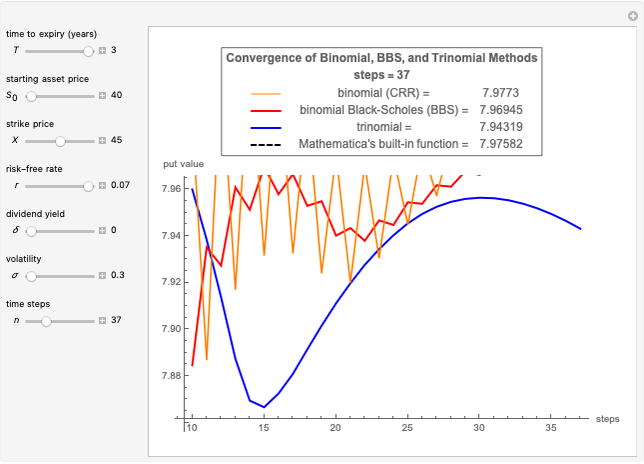
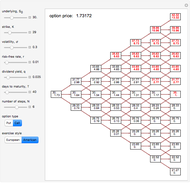
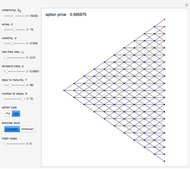
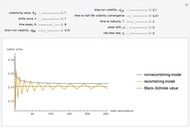
When you choose the number of time steps, the Demonstration calculates expected values from the models for that number of time steps and each number of time steps preceding it.

The number of time steps you set relates only to the nonrecombining approach. Once chosen, the total number of calculations needed to calculate the value is found. In the nonrecombining case, there are 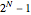calculations after all the possible prices have been calculated and maximums taken at the terminal nodes (i.e., once the process for the underlying value has been estimated using the binomial tree).

Following this, the total number of calculations is used to solve how many time steps the recombining approach would use to match that number of total calculations. For instance, if 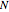is chosen to be 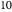, there are 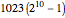calculations required by the nonrecombining approach. The Demonstration takes 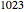and solves 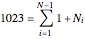for 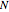(the total number of calculations for the recombining approach given 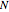time steps). In this case, the closest number of time steps that yields this number of calculations is 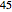(giving 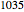total calculations). Therefore, when the nonrecombining approach is set at 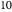time steps (and the Demonstration depicts 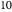expected value calculations), the recombining approach will be set at 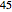time steps and depict 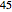expected value calculations. This is done simply to enhance the visual descriptiveness of the Demonstration.

For the estimation of the Black–Scholes value, note that we cannot estimate the volatility for the process of the underlying asset through time as it is not constant (that is, we cannot directly estimate the process for 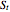). However, we can estimate the distribution of 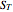(the terminal value; see [3]). This means that we can calculate a volatility of the terminal value of the underlying asset. The volatility calculation in the original Demonstration after moves is:

.

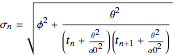For the Black–Scholes estimation this simply reduces to:

.

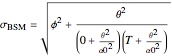References

[1] G. Guthrie, "Learning Options and Binomial Trees," Wilmott Journal: The International Journal of Innovative Quantitative Finance Research, 3(1), 2011 pp. 1–23. doi:10.1002/wilj.42.

[2] J. C. Cox, S. A. Ross, and M. Rubinstein, "Option Pricing: A Simplified Approach," Journal of Financial Economics, 7(3), 1979 pp. 229–263. doi:10.1016/0304-405X(79)90015-1.

[3] J. C. Hull, Options, Futures, and Other Derivatives, 8th ed., Boston: Prentice Hall, 2012.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send