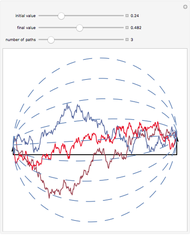
Correlated Gamma Variance Processes with Common Subordinator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
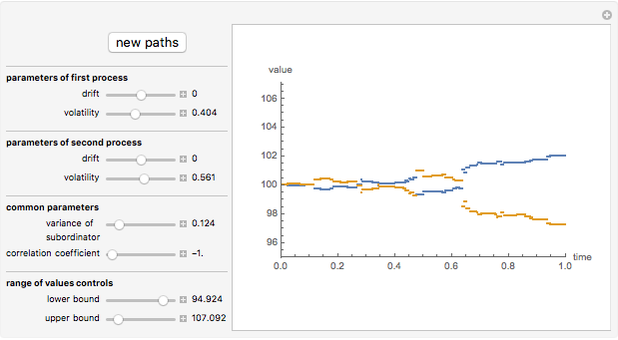
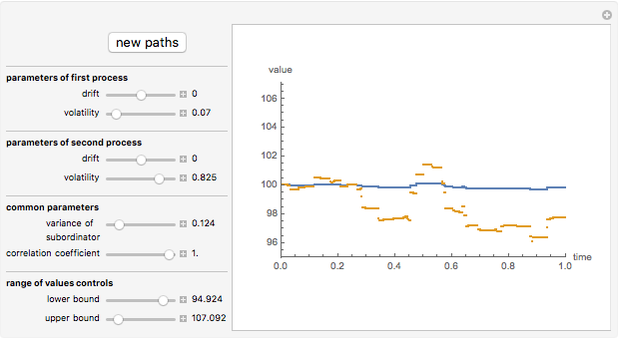
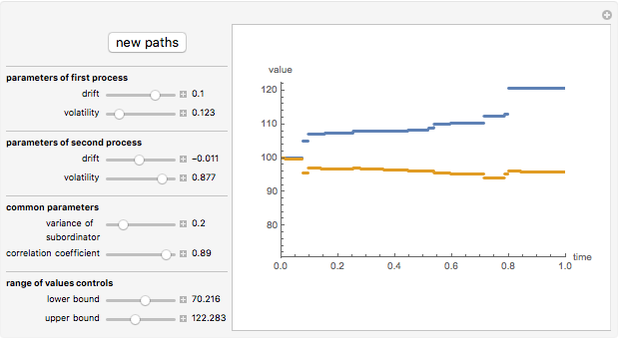
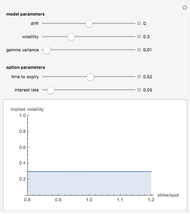
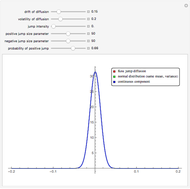
This Demonstration shows the movements of the prices of two stocks given by exponential correlated Brownian motion that are time-changed with the same gamma process subordinator. In other words, the stock prices are given by two correlated exponential variance gamma Lévy processes whose large jumps tend to occur at the same time.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Ever since Benoit Mandelbrot's seminal paper [1] introduced Lévy processes into the modeling of asset prices, a debate has raged among researchers in mathematical finance about the need to include discontinuous jumps in such models. The implications of this assumption are quite dramatic, particularly for such basic practices as hedging [3]. Statistical tests have given strong support for the presence of discontinuous jumps [2]. The financial crisis of 2008 is seen by many as vindicating the view that unpredictable and unhedgeable jumps are omnipresent in stock market prices and that most of market risk is concentrated in these jumps. However, modelling jump processes still offers many difficult challenges. One of them is that practical financial applications usually require multidimensional models, which are much easier to construct in the classical exponential Brownian motion setting. Here we demonstrate one of the simplest ways to construct two correlated jump processes: by using two correlated Brownian motions with a common subordinator. The subordinator chosen is a gamma process, so the two motions are (exponential) Variance Gamma processes. The advantage of this approach is its simplicity; the disadvantage is that the two processes can never be made truly independent in this way, since due to the common subordinator they tend to have their large jumps happen at the same times. This method, however, can be useful in modelling the so-called "systemic risk" that affects all stocks at the same time.
More sophisticated (and more complicated) approaches are based on the concept of a Lévy copula.
References:
[1] B. Mandelbrot, "The Variation of Certain Speculative Prices," Journal of Business, XXXVI, 1963 pp. 392–417.
[2] Y. Ait–Sahalia and J. Jacod, "Testing for Jumps in a Discretely Observed Process," The Annals of Statistics, 37(1), 2009 pp. 184–222.
[3] R. Cont and P. Tankov, Financial Modelling with Jump Processes, New York: CRC Press, 2004.