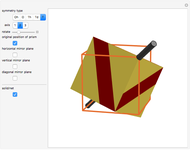
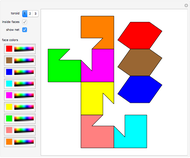
Dehn Invariant of Some Disjoint Unions of Polyhedra with Icosahedral Symmetry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Two sets  and
and  are equidecomposable (can be dissected into each other) if there are two families of sets
are equidecomposable (can be dissected into each other) if there are two families of sets  and
and  ,
,  , such that
, such that  , the interiors of the
, the interiors of the  are disjoint,
are disjoint,  , the interiors of the
, the interiors of the  are disjoint, and
are disjoint, and 
 is congruent to
is congruent to  ). More intuitively,
). More intuitively,  can be cut up into finitely many pieces that can be rearranged to form
can be cut up into finitely many pieces that can be rearranged to form  ; here the pieces should be polyhedra.
; here the pieces should be polyhedra.
Contributed by: Izidor Hafner (October 2014)
Open content licensed under CC BY-NC-SA
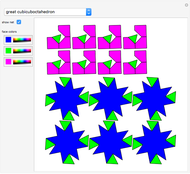
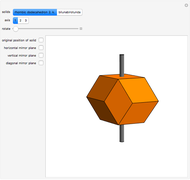
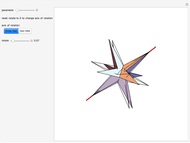
Snapshots
Details
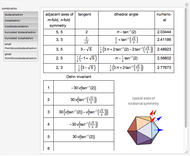
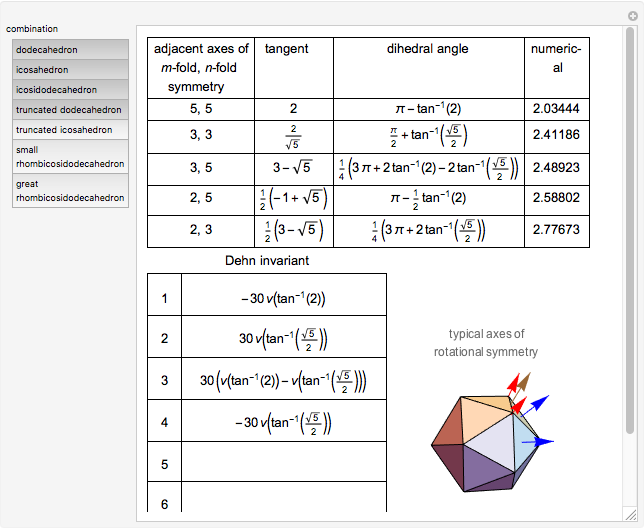
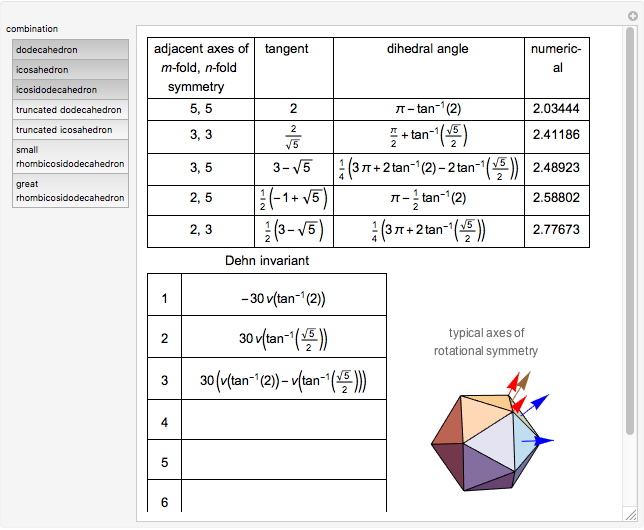
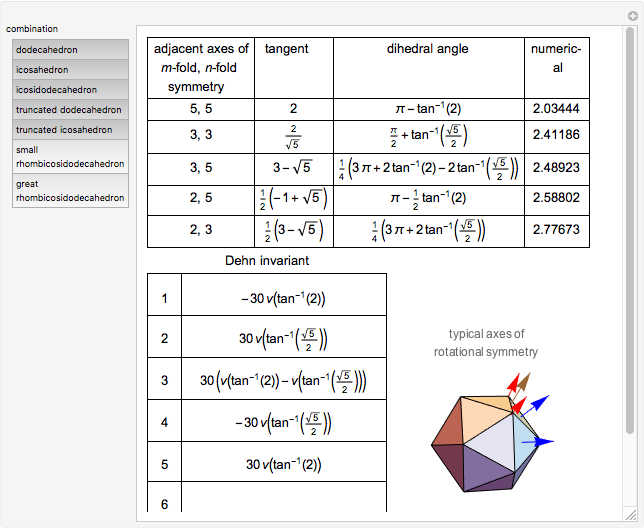
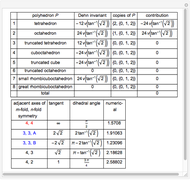
That some combinations of Platonic and Archimedean solids have Dehn invariant 0 was shown in [1].
Reference
[1] J. H. Conway, C. Radin, and L. Sadun, "On Angles Whose Squared Trigonometric Functions Are Rational," Discrete & Computational Geometry, 22(3), 1999 pp. 321–332. doi:10.1007/PL00009463.
[2] N. Do, "Mathellaneous," Gazette of the Australian Mathematical Society, 33(2), 2006 pp. 81–87. www.austms.org.au/Publ/Gazette/2006/May06/mathellaneous.pdf.
Permanent Citation