Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Escape to Infinity

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

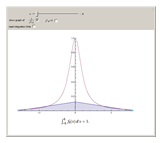
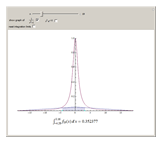
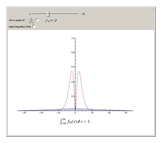
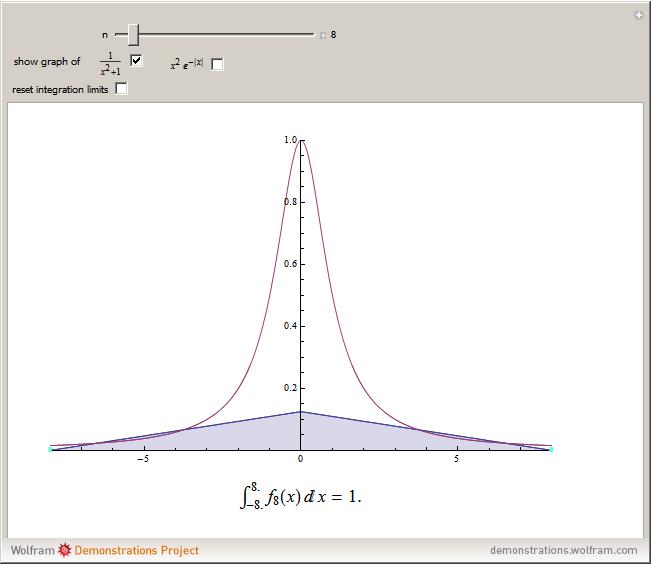
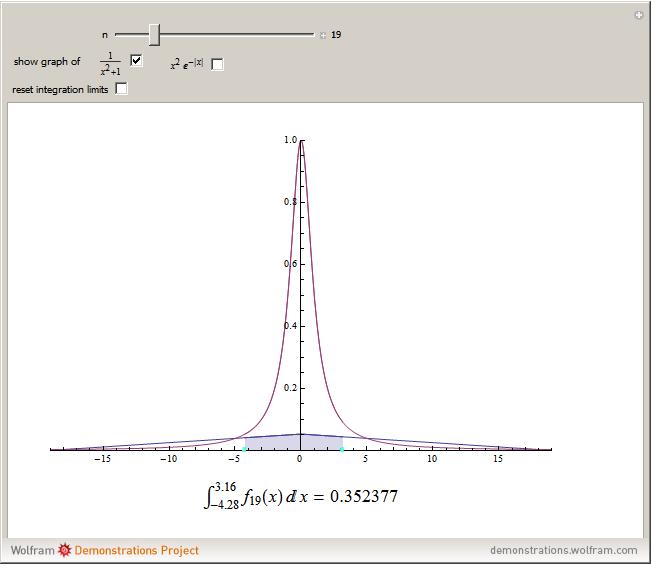
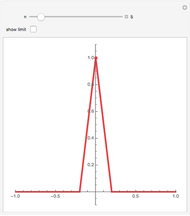
This Demonstration shows a family of continuous functions that converge uniformly to the zero function on the real line but whose integrals are all equal to 1. Thus, the limit of the integrals over the real line is not the integral of the limits. However, by fixing the endpoints (the movable bluish points on the real axis) and then increasing , you see that the integrals over a fixed finite interval do tend to 0.

[more]

Moreover, by the dominated convergence theorem, such a family of functions cannot be simultaneously bounded (over almost all the real line) by an integrable function. We illustrate this by showing two examples of functions that have a finite integral over the whole real line, which fail to bound for large enough . The two examples are , whose integral is equal to , and , whose integral is equal to 4. The graphs of both functions "eventually" fall below the graph of for large enough and large enough values of .

[less]

Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Let be a sequence of continuous real functions on a closed interval . Suppose the sequence converges uniformly to a function . Then is continuous and (Riemann integral). The Demonstration shows that this is not true if the interval is replaced by the entire real line. The sequence of functions shown is given by

Then for all , , although the sequence converges uniformly on to the zero function. However, by choosing real numbers , with (represented by the blue points on the axis) we see that as . The phenomenon of nonconvergence to 0 of integrals of functions that converge uniformly to 0 on is sometimes called "escape to infinity" (e.g. see [1]).

The dominated convergence theorem (see [1]) states that if there exists a function with for all large enough values of and and such that , then the above cannot happen, since in this case we always have .

Reference

[1] T. W. Körner, A Companion to Analysis:A Second First and First Second Course in Analysis, Graduate Studies in Mathematics vol. 62, American Mathematical Society, 2004.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send