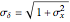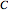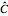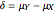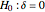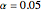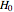Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Exploring Robustness of Mean-Difference Confidence Intervals

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

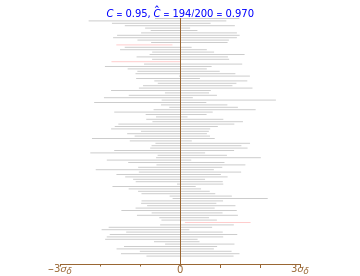
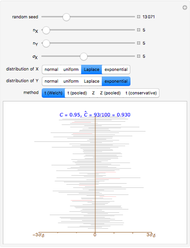
This Demonstration examines confidence intervals at the 95% level for the difference in means in random samples and 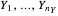from either a normal, uniform, Laplace, or centered exponential distribution. The distributions all have mean 0. The variance of the 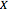distribution can be varied from 1 to 10 and the variance of is fixed at 1. Several methods available in the Mathematica function MeanDifferenceCI are examined. The "t (Welch)" method is the default method with MeanDifferenceCI, "t (pooled)" corresponds to the option setting 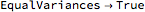, while "Z" and "Z (pooled)" correspond to setting the option KnownVariance to the sample variances of 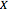and or else to the pooled variance estimate. The fifth method is a conservative approximation using the two-sample t-statistic with degrees of freedom equal to .

[more]

The scaling on the horizontal axis is in terms of , the standard deviation of .

Each iteration shows 100 confidence intervals, the nominal coverage probability , and the empirical coverage probability . By changing the random seed, more confidence intervals are produced and an increasingly accurate estimate of the true coverage probability is obtained. Try doing at least 10,000 simulations.

If the true coverage probability is greater than the nominal one, in this case set to 95% in our initialization code, the method is said to be conservative. Ideally the empirical coverage probability should be close to the nominal value. As an approximation, conservative confidence intervals are much more acceptable than ones that are not.

Using this Demonstration you can easily find that the "t (pooled)" method is not conservative when the variances are not equal. Also the -methods do not work well unless the sample sizes are quite large. Overall the "t (Welch)" works best even though it is also an approximation. The "t (pooled)" is exact for normal populations with equal variances but is not recommended since it is not robust when this assumption does not hold. The loss in degrees of freedom with the assumption of unequal variances is usually not as important.

The 95% confidence interval for is equivalent to a test of the null hypothesis versus at level . The empirical type I error rate is estimated by . The red lines correspond to cases where is rejected at the 5% level.

[less]

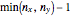Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

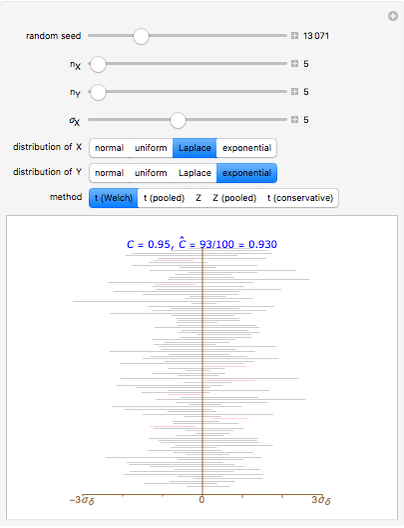
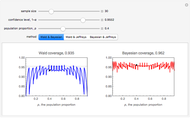
Snapshot 1: Using "t (Welch)", setting 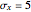, , 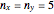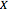's from Laplace and 's from centered exponential distribution, we find after about 10,000 simulations ; in this case the "t (Welch)" method is robust. Using "Z" or "Z pooled", 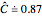after about 10,000 simulations, so clearly the -methods are not suitable using estimated standard deviations.

Snapshot 2: As in Snapshot 1, except the roles of and are reversed; in this case 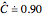after 10,000 simulations and we conclude even "t (Welch)" is not robust. Increasing the sample sizes, , we obtain 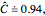so for large enough samples, "t (Welch)" is accurate.

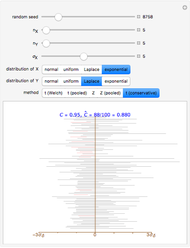
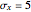Snapshot 3: Assuming and both normal, setting , and selecting "t (pooled)", we find after 10,000 simulations that 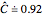; instead of 95% coverage, it is less. The "t (pooled)" intervals err on the side of not being conservative, that is, they are too narrow; for this reason, the use of the "t (pooled)" method is disparaged; see p. 487 of [1].

Snapshot 4: With 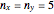, , 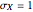both 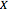and normal, and using the "t (conservative)" method, after 10,000 simulations, 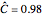, showing that this method is indeed conservative.

Snapshot 5: Settings as in Snapshot 1 but using the 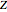-method; after 10,000 simulations 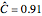, showing that this method is not conservative and not acceptable with small samples. Increasing 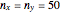, 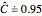after 10,000 simulations, showing that for larger samples the 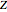-method is sufficiently accurate.

Some textbooks recommend using the pooled t-test if a simple 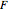-test for equal variances is not rejected. As noted on p. 488 of [1], this is not a good idea, because this test itself is not robust against skewness and/or outliers.

The robustness for other confidence levels could be explored by resetting the variable in the initialization code.

[1] D. S. Moore, The Basic Practice of Statistics, 5th. ed., New York: W. H. Freeman and Company, 2010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send