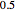Flow of a Carreau Fluid in a Circular Tube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
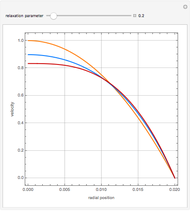
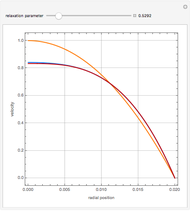
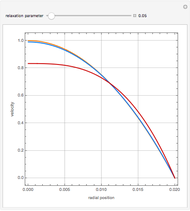
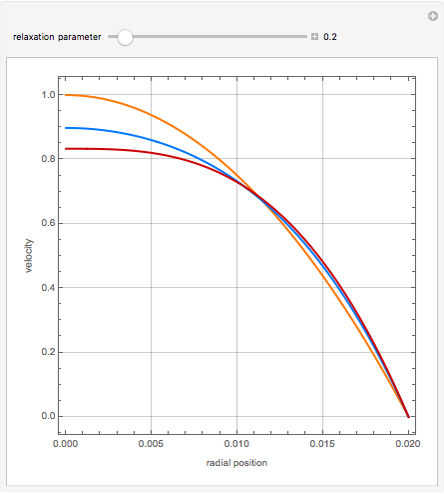
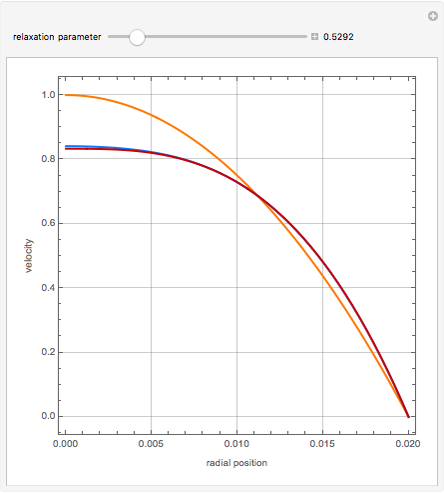
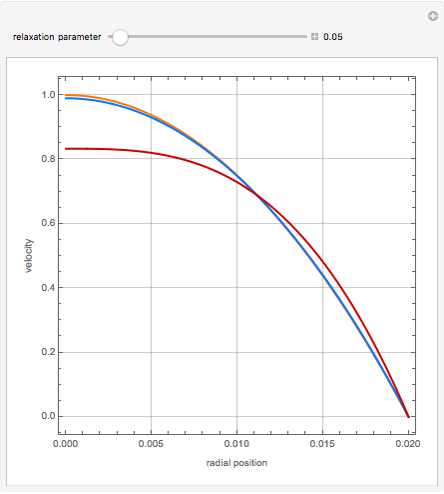
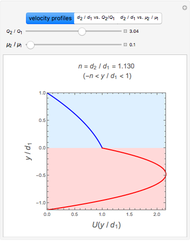
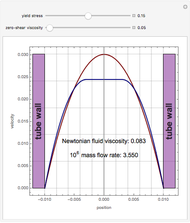
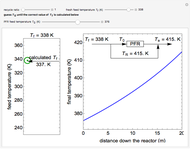
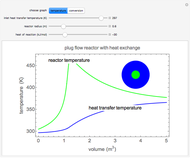
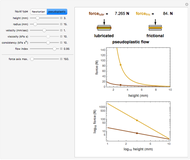
A Carreau fluid is a generalized type of Newtonian fluid in which viscosity depends upon shear rate,  .
.
Contributed by: Housam Binous (December 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
According to the Carreau model, first proposed by Pierre Carreau,
 .
.
For  , this reduces to a Newtonian fluid with
, this reduces to a Newtonian fluid with  .
.
For  , we obtain a power-law fluid with
, we obtain a power-law fluid with  .
.
References:
[1] H. Binous,"Introducing Non-Newtonian Fluid Mechanics Computations with Mathematica in the Undergraduate Curriculum," Chemical Engineering Education, 41(1), 2007 pp. 59–64.
[2] J. O. Wilkes, Fluid Mechanics for Chemical Engineers, Upper Saddle River, NJ: Prentice Hall, 1999.
Permanent Citation