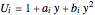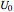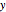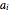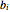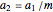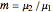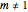Plane Poiseuille Flow of Two Superposed Fluids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
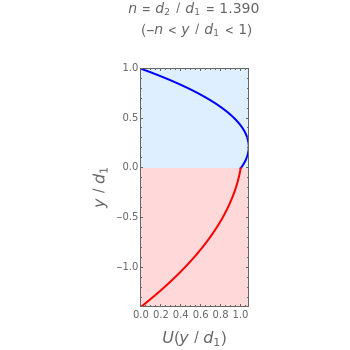
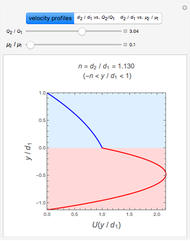
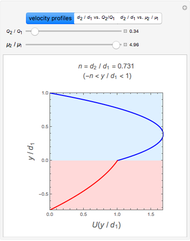
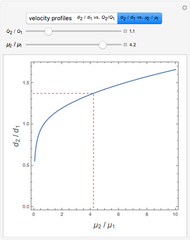
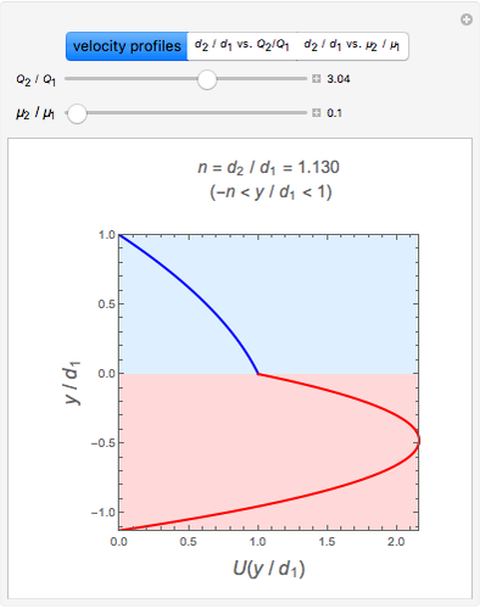
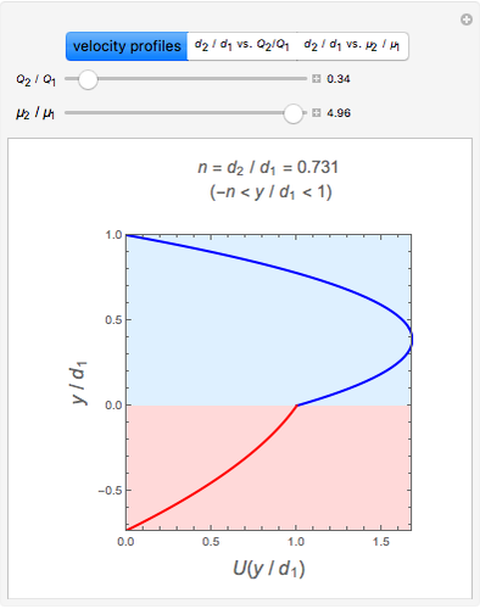
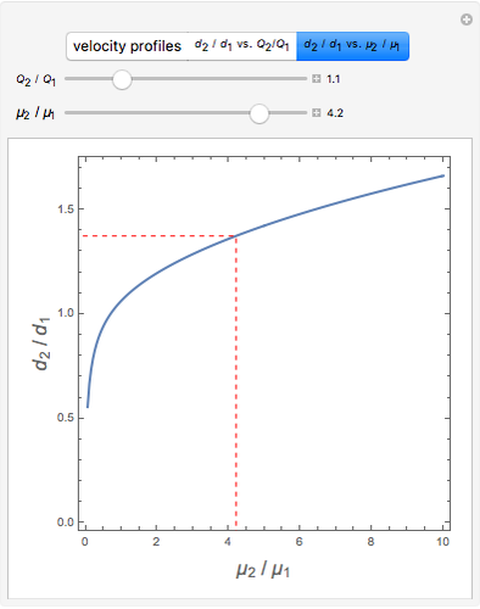
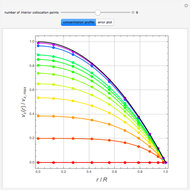
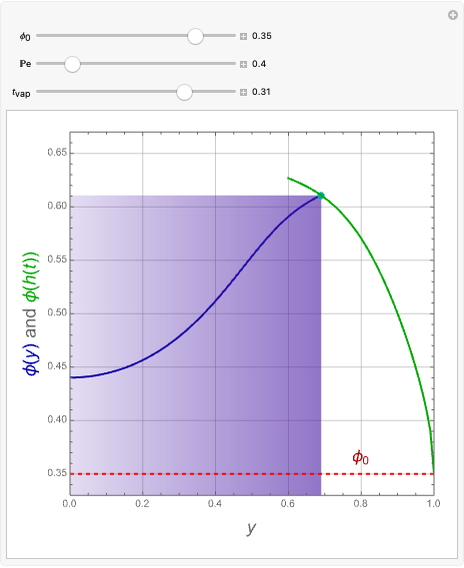
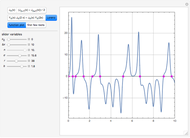
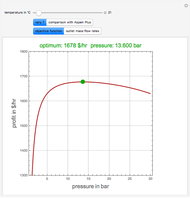
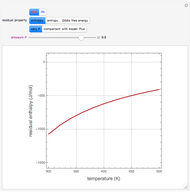
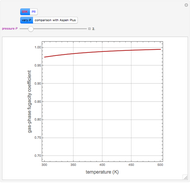
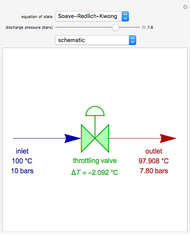
This Demonstration analyzes plane Poiseuille flow of two superposed fluids. For a specified channel, the rectilinear flow field is defined by four parameters: two viscosities 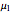 and
and  and two volumetric flow rates
and two volumetric flow rates  and
and  . Conservation of mass then determines the location of the liquid-liquid interface in the channel, which can be expressed as a thickness ratio
. Conservation of mass then determines the location of the liquid-liquid interface in the channel, which can be expressed as a thickness ratio  .
.
Contributed by: Brian G. Higgins and Housam Binous (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] S. G. Yiantsios and B. G. Higgins, "Linear Stability of Plane Poiseuille Flow of Two Superposed Fluids," Physics of Fluids, 31(11), 1988 pp. 3225–3238. doi:10.1063/1.866933.
Permanent Citation