Pulsatile Flow in a Circular Tube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
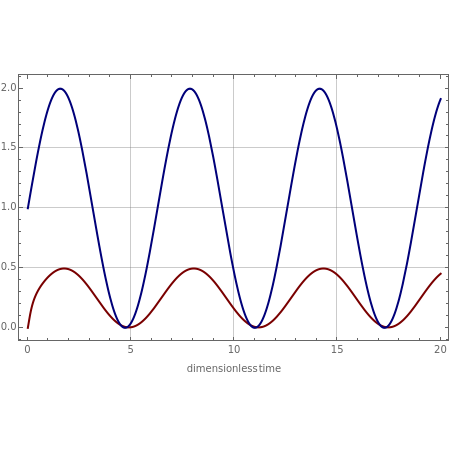
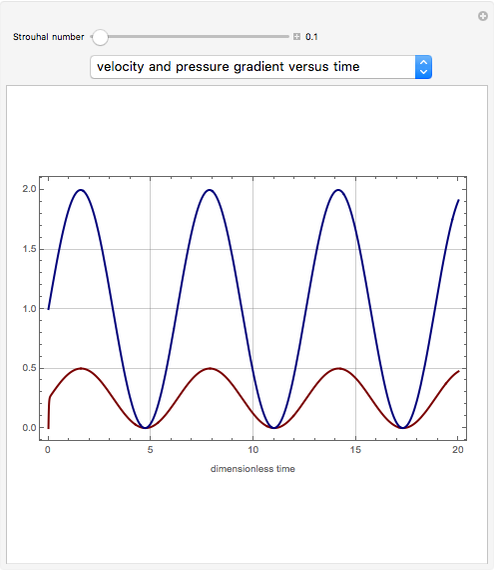
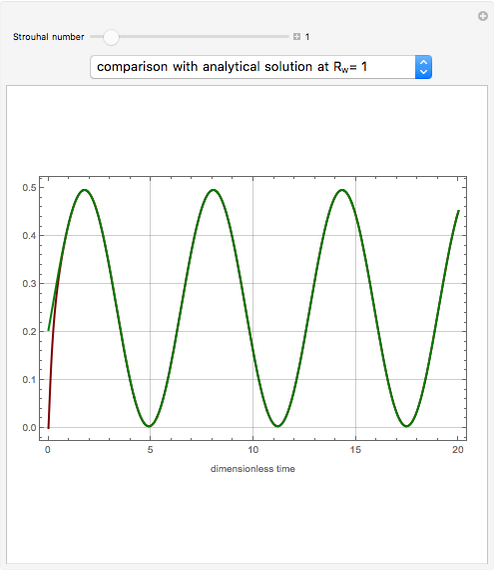
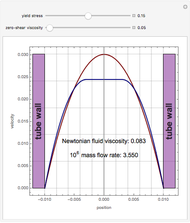
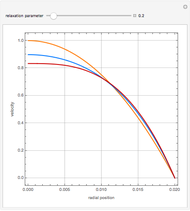
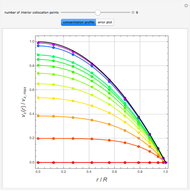
The velocity distribution,  , is computed numerically using NDSolve for a pulsatile pressure-driven flow in a tube. This model considerably simplifies the actual flow through veins and arteries.
, is computed numerically using NDSolve for a pulsatile pressure-driven flow in a tube. This model considerably simplifies the actual flow through veins and arteries.
Contributed by: Housam Binous and Brian G. Higgins (March 2011)
Open content licensed under CC BY-NC-SA
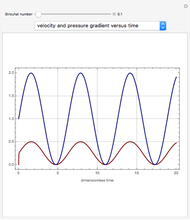
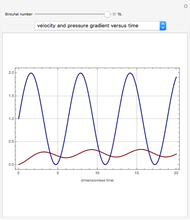
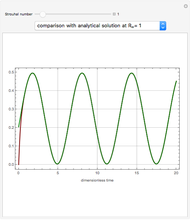
Snapshots
Details
The oscillating pressure-driven flow in a tube obeys the following equations:
- ,
,
ρ ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,
 ,
,  ,
,  , and
, and  ,
,
where  ,
,  , and
, and  are the dimensionless velocity, radial position, and time.
are the dimensionless velocity, radial position, and time.
The variable  can be considered as a Reynolds number, since it appears as the ratio of inertial forces to viscous forces. There are two characteristic times for this problem:
can be considered as a Reynolds number, since it appears as the ratio of inertial forces to viscous forces. There are two characteristic times for this problem:  , the period of the imposed pressure gradient, and
, the period of the imposed pressure gradient, and  , the time for diffusion of momentum across the tube.
, the time for diffusion of momentum across the tube.
References
[1] L. G. Leal, Laminar Flow and Convective Transport Processes, Boston: Butterworth–Heinemann, 1992.
[2] L. G. Leal, Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes, Cambridge: Cambridge University Press, 2007.
Permanent Citation