Generalized Hyperbolic Distribution
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
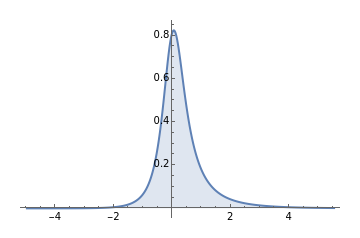
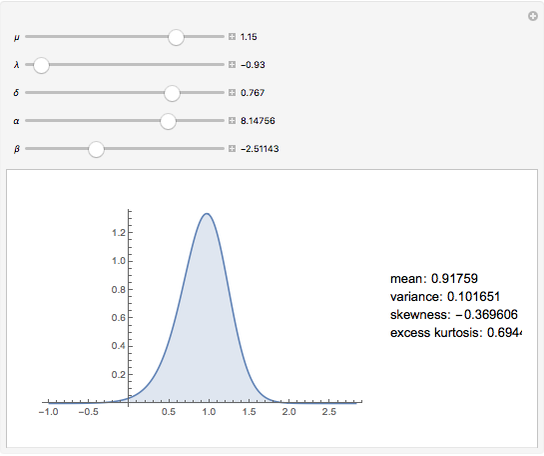
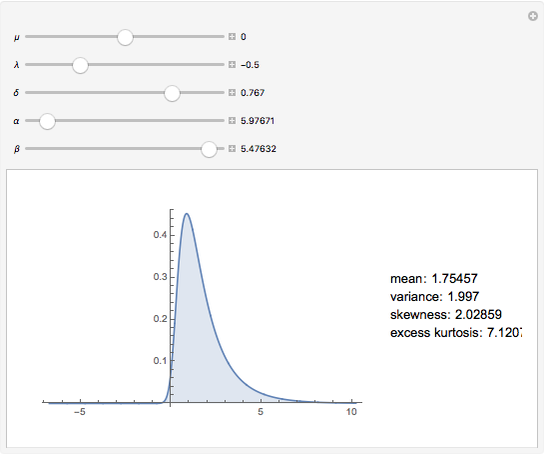
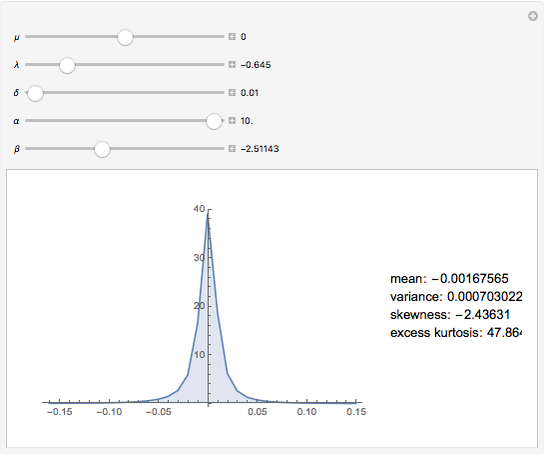
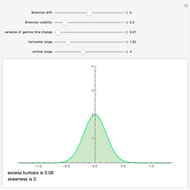
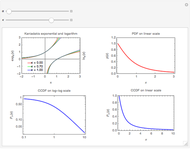
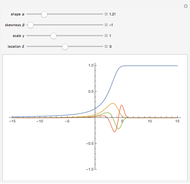
This Demonstration shows the probability density function of the generalized hyperbolic distribution, which generalizes a large number of distributions with numerous applications in finance and other areas. There are a number of parametrizations of this distribution. We use the most common one with five parameters, of which 
and 
describe the location and the scale, while 
and 
determine the shape of the distribution. Special values of the parameter 
often correspond to well-known special cases: for example, 
gives the hyperbolic distribution and 
gives the normal inverse Gaussian (NIG) distribution. On the other hand, the case 
gives the variance gamma distribution. Many other distributions are obtained as limiting cases.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
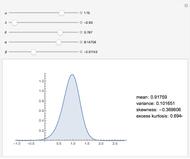
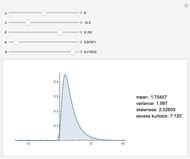
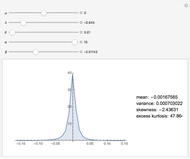
Snapshots
Details
Generalized hyperbolic distributions were introduced by Barndorff–Nielsen [1]. They generalize many previously known distributions in addition to being a source of many new ones. As they are infinitely divisible, Lévy and other stochastic processes can be based on them.
Such processes were first applied in finance by Eberlein and Keller [2]. Being normal variance-mean mixtures, GH distributions possess semi-heavy tails and allow for a natural definition of volatility models by replacing the mixing generalized the inverse Gaussian (GIG) distribution by appropriate volatility processes.
[1] O. E. Barndorff-Nielsen, "Exponentially Decreasing Distributions for the Logarithm of Particle Size," Proceedings of the Royal Society London A, 353(1674), 1977 pp. 401–419.
[2] E. Eberlein and U. Keller, "Hyperbolic Distributions in Finance," Bernoulli 1(3), 1995 pp. 281–299.
Permanent Citation
The Return Distribution of the Variance Gamma Process
Andrzej Kozlowski
Two Jump Diffusion Processes
Andrzej Kozlowski
The Poisson Process
Andrzej Kozlowski
Merton's Jump Diffusion Model
Andrzej Kozlowski
Brownian Bridge
Andrzej Kozlowski
Correlated Wiener Processes
Andrzej Kozlowski
Correlated Gamma Variance Processes with Common Subordinator
Andrzej Kozlowski
The Kappa Distribution
Fabio Clementi
Autoregressive Moving-Average Generator
Matus Baniar
Stable Distribution Function
Bob Rimmer
-
The Black-Scholes European Call Option Formula Corrected Using the Gram-Charlier Expansion
Andrzej Kozlowski -
Option Prices in the Kou Jump Diffusion Model
Andrzej Kozlowski -
The Polar and Bipolar of a Convex Polytope
Andrzej Kozlowski -
Two Jump Diffusion Processes
Andrzej Kozlowski -
The Vieta Mapping for the Coxeter Group A_2
Andrzej Kozlowski -
The Bifurcation Set of the Space of Smooth Real Functions
Andrzej Kozlowski -
The Swallowtail Singularity
Andrzej Kozlowski -
Singularities of an Ellipsoidal Wave Front
Andrzej Kozlowski -
Nonuniqueness of Option Pricing Under the Meixner Model
Andrzej Kozlowski -
Coin Machine
Andrzej Kozlowski -
A Mean-Reverting Jump Diffusion Process
Andrzej Kozlowski -
Standard American and European Options
Andrzej Kozlowski -
Density of the Kou Jump Diffusion Process
Andrzej Kozlowski -
The Meixner Process
Andrzej Kozlowski -
Fitting the Meixner Distribution to S&P 500 Returns
Andrzej Kozlowski -
Simple Graphs and Their Binomial Edge Ideals
Andrzej Kozlowski -
The Eneström-Kakeya Bounds for Roots of a Polynomial with Positive Coefficients
Andrzej Kozlowski -
Newton Polygon and Branching of Algebraic Curves
Andrzej Kozlowski -
Counting the Number of Roots of Transcendental Functions in Bounded Regions Using Winding Numbers
Andrzej Kozlowski -
The Space of Inner Products
Andrzej Kozlowski