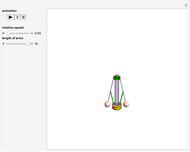
Kempe's Universality Theorem: An Example

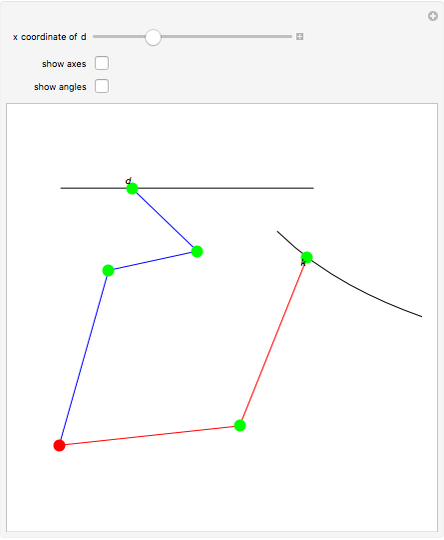
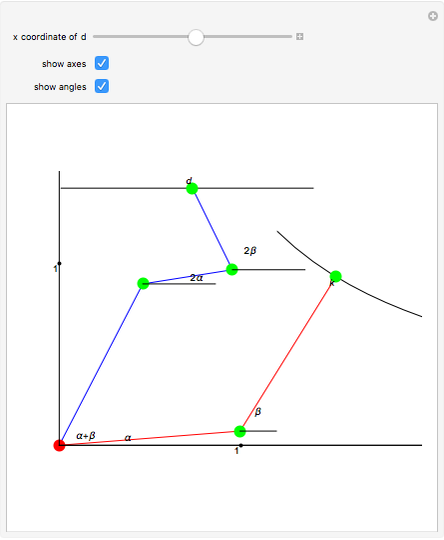
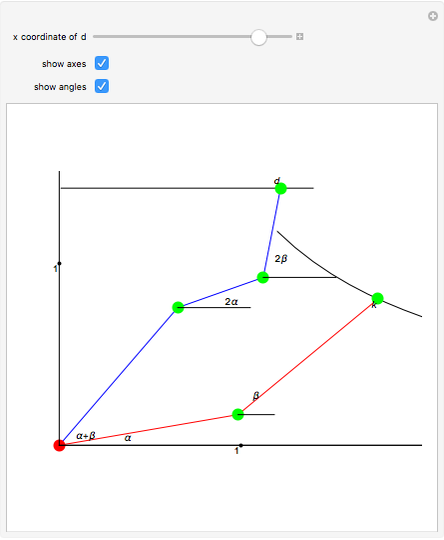
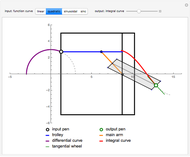
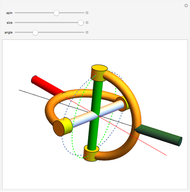
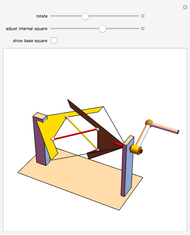
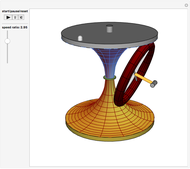
Roughly, Kempe's universality theorem states that any finite part of a plane algebraic curve can be traced out by a vertex of some linkage. This Demonstration illustrates a particular example: there exists a linkage such that, if the point is forced to move on the straight line , the point moves on the hyperbola .

On the curve, , so that .