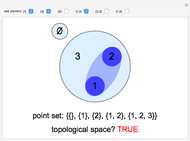
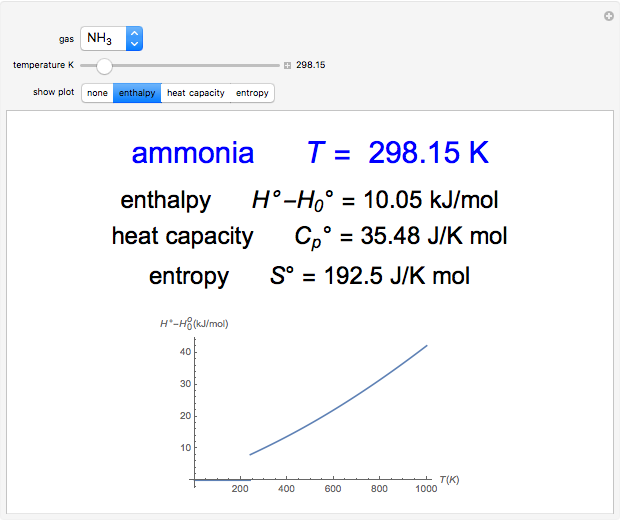
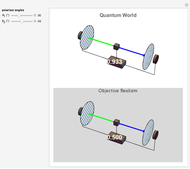
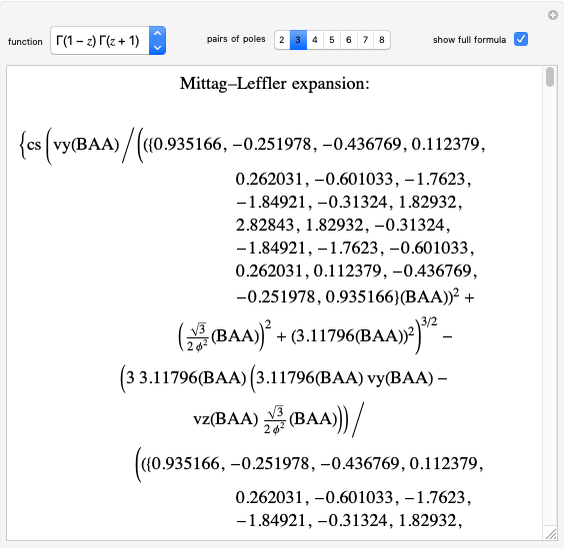
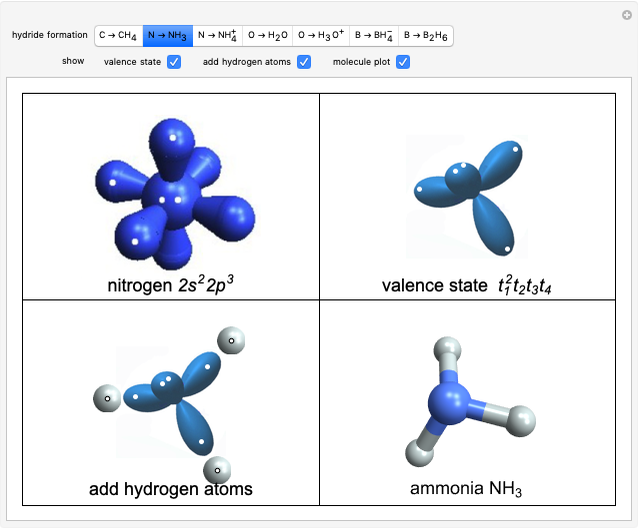
Lensmaker's Equation

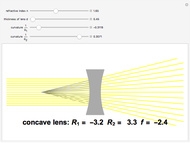
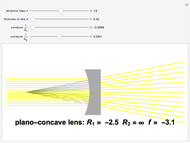
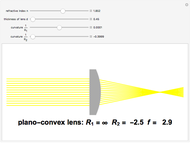
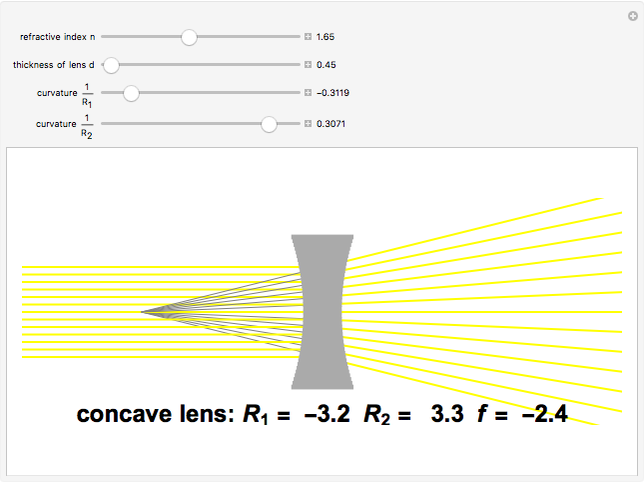
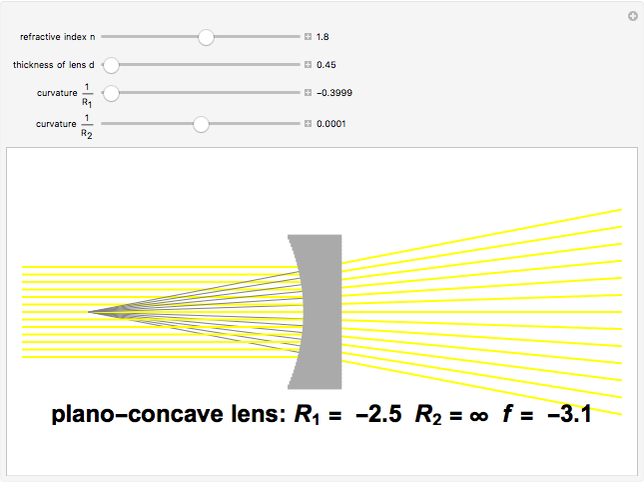
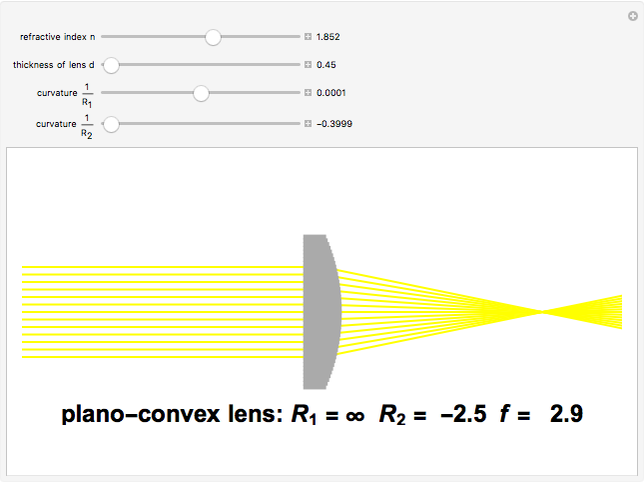
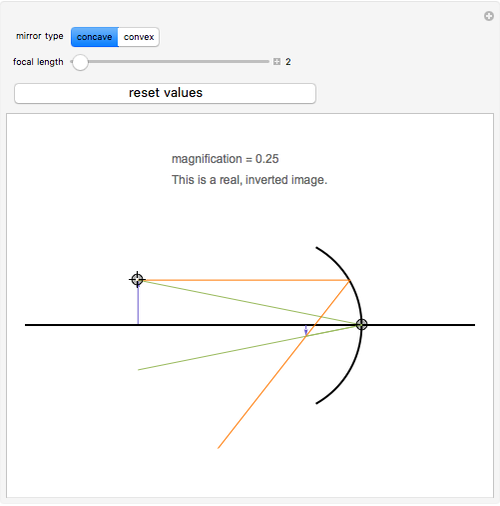
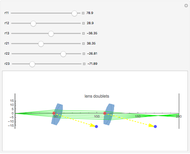
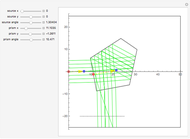
The lensmaker's equation relates the focal length of a simple lens with the spherical curvature of its two faces:
,
where and represent the radii of curvature of the lens surfaces closest to the light source (on the left) and the object (on the right). The sign of is determined by the location of the center of curvature along the optic axis, with the origin at the center of the lens. Thus for a doubly convex lens, is positive while is negative.

The focal length is positive for a converging lens but negative for a diverging lens, giving a virtual focus, indicated by a cone of gray rays.

The lens index of refraction is given by . Optical-quality glass has in the vicinity of 2.65. The top slider enables you to vary between 1.0008, its value for air, and 3.42, the refractive index of diamond.

The width represents the distance between the faces of the lens along the optical axis. The value of is restrained by the slider so that the lens faces never intersect anywhere.

The parameters , , and are to be expressed in the same length units, often cm. The reciprocal is known as the optical power of the lens, expressed in diopters . A converging lens, as shown in the thumbnail, can serve as a simple magnifying glass.

In the thin-lens approximation, the lens width is small compared to the other lengths and the lensmaker's equation can be simplified to .