Lines of Force for Two Point Charges

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
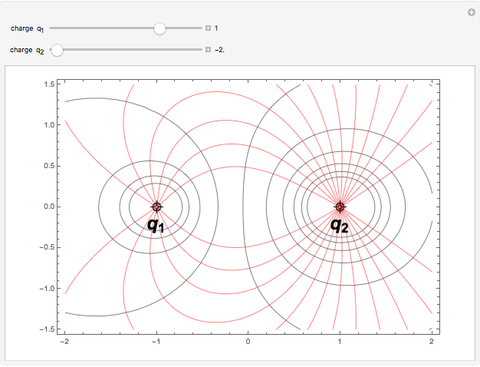
In an earlier Demonstration by Stephen Wolfram, two-dimensional equipotential contours  , representing cross sections of equipotential surfaces, were plotted for two point charges of variable magnitude and location. It was also possible to make a vector plot of the corresponding electric field
, representing cross sections of equipotential surfaces, were plotted for two point charges of variable magnitude and location. It was also possible to make a vector plot of the corresponding electric field  . It is much trickier to plot the lines of force emanating from a positive point charge and converging on a negative point charge. These are everywhere tangent to the electric field vectors and form a set of contours
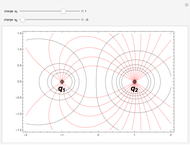
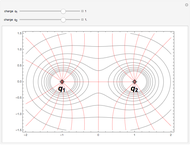
. It is much trickier to plot the lines of force emanating from a positive point charge and converging on a negative point charge. These are everywhere tangent to the electric field vectors and form a set of contours  , shown as red curves, everywhere orthogonal to the equipotentials
, shown as red curves, everywhere orthogonal to the equipotentials  , shown in gray.
, shown in gray.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: lines of force for two unequal charges of opposite sign
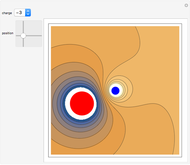
Snapshot 2: repulsion between like charges
Snapshot 3: lines of force for a point dipole, obtained for two infinitesimally separated opposite charges
Permanent Citation