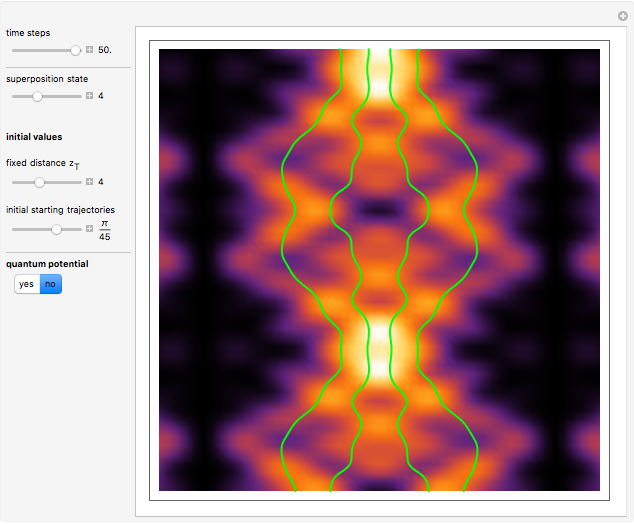
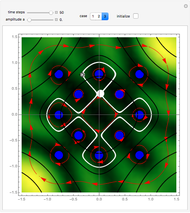
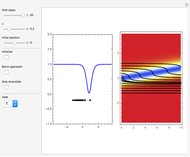
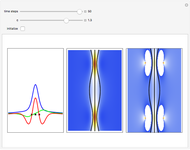
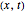Time Evolution of Optical Rogue Waves (Rogons) in the Causal Interpretation of Quantum Mechanics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
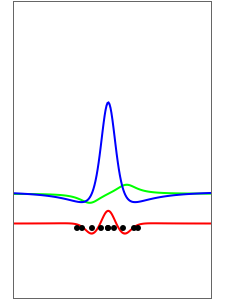
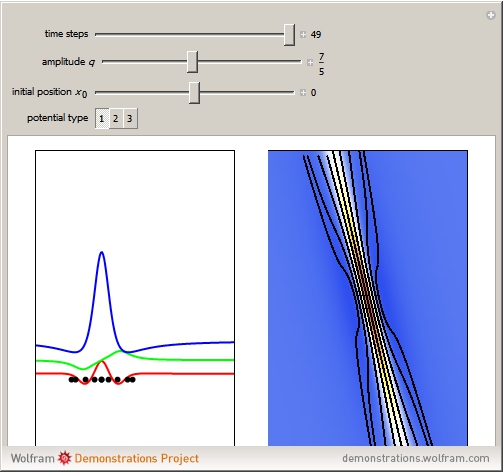
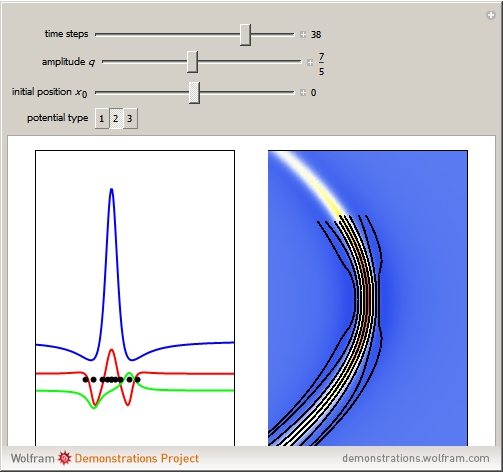
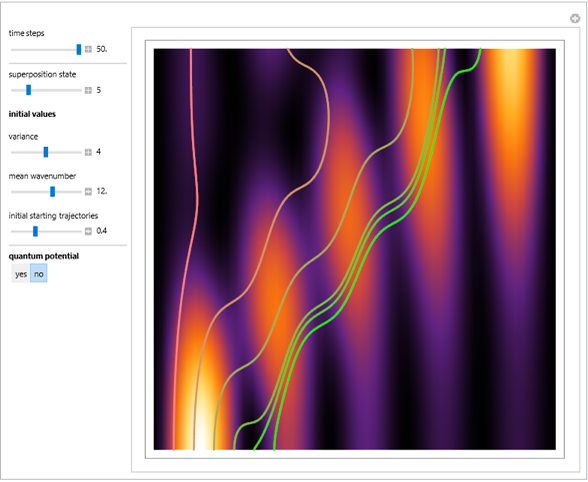
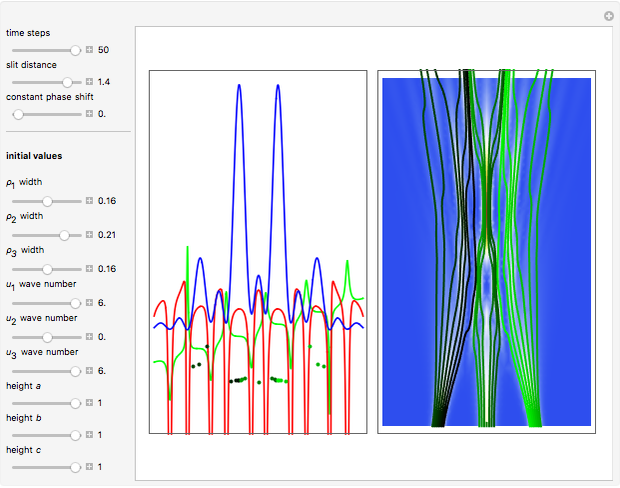
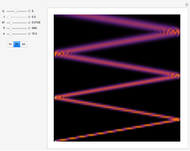
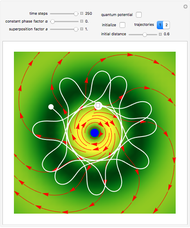
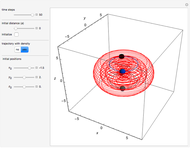
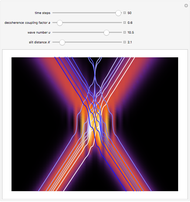
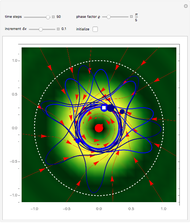
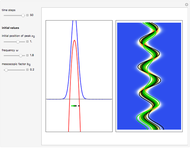
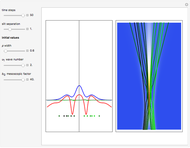
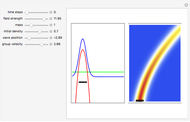
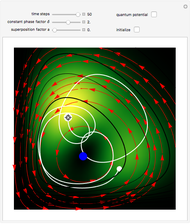
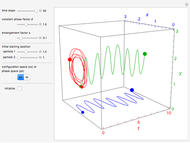
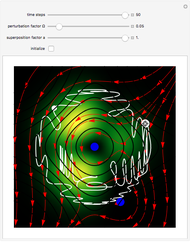
In this Demonstration, modified Peregrine solitons resembling optical rogue waves (here called rogons) are studied in the causal interpretation of L. de Broglie and D. Bohm. The rogons have a variable function and a variable initial position (for the first case). The word rogon has its origin in physical similarities between the rogue waves and solitary wave. If the waves reappear virtually unaffected in size or shape shortly after their interactions, Yan [1, 3] called them "rogons".
[more]
Contributed by: Klaus von Bloh (January 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For simplicity, the homogeneous nonlinear Schrödinger equation with only one variable coefficient is taken for the evaluation of the de Broglie–Bohm trajectories [1]:
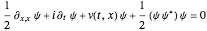 ,
,
with 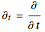 and so on, where
and so on, where  is a complex function and
is a complex function and 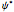
 is its complex conjugate.
is its complex conjugate.
The causal interpretation introduced trajectories that are guided by a real phase function determined by the wavefunction. In the eikonal representation of the wave, 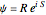 , the gradient of the phase
, the gradient of the phase 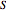 is the particle velocity
is the particle velocity 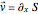 . In this interpretation, the origin of the motion of the particle is the potential
. In this interpretation, the origin of the motion of the particle is the potential 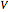 , given by
, given by 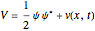 , plus an additional term
, plus an additional term 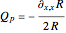 . The latter may be interpreted alternatively as a kind of fluid pressure or quantum Bohm potential.
. The latter may be interpreted alternatively as a kind of fluid pressure or quantum Bohm potential.
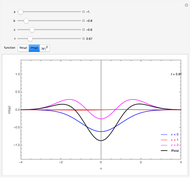
For this Demonstration the three functions 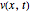 and
and  are
are
(1) 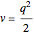 and
and 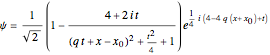 ,
,
(2) 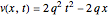 and
and 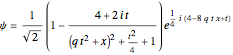 ,
,
(3) 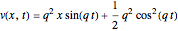 and
and 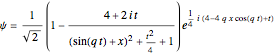 ,
,
where  is a free parameter and
is a free parameter and 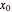 is the initial position of the peak of the wave. For the first two cases there are analytical solutions for the trajectories; let
is the initial position of the peak of the wave. For the first two cases there are analytical solutions for the trajectories; let 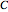 be an integration constant. The initial positions are estimated by solving the equation
be an integration constant. The initial positions are estimated by solving the equation 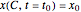 numerically. Real-valued trajectories are obtained for several
numerically. Real-valued trajectories are obtained for several  's. The starting positions of the particles are linearly distributed around the peak of the wave at
's. The starting positions of the particles are linearly distributed around the peak of the wave at  and
and  (
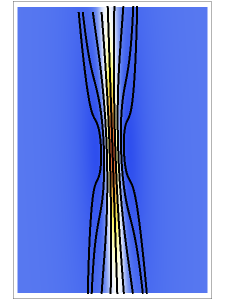
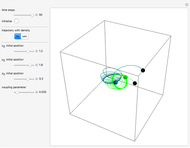
( only for the first case). Due to insufficient decrease in the merit function of the integration constant in the analytic functions of the trajectories, only the positive initial positions (right from the peak) are evaluated, through Mathematica's built-in function FindRoot. The trajectories for the negative initial positions (left from the peak) are computed numerically by Mathematica's built-in function NDSolve. You can control the paths together with the starting points by changing the initial condition
only for the first case). Due to insufficient decrease in the merit function of the integration constant in the analytic functions of the trajectories, only the positive initial positions (right from the peak) are evaluated, through Mathematica's built-in function FindRoot. The trajectories for the negative initial positions (left from the peak) are computed numerically by Mathematica's built-in function NDSolve. You can control the paths together with the starting points by changing the initial condition 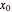 . The path
. The path 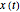 together with the starting point leads to a trajectory in
together with the starting point leads to a trajectory in 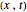 -space.
-space.
References
[1] Z. Yan, "Nonautonomous 'Rogons' in the Inhomogeneous Nonlinear Schrödinger Equation with Variable Coefficients," Physics Letters A, 374, 2010 pp. 672–679.
[2] W. Xiao-Chun, H. Jing-Song, and L. Yi-Shen, "Rogue Wave with a Controllable Center of Nonlinear Schrödinger Equation," Communications in Theoretical Physics, 56, 2011 pp. 631–637.
[3] Z. Yan. "Optical Rogue Waves (Rogons)." The Wolfram Demonstrations Project. demonstrations.wolfram.com/OpticalRogueWavesRogons.
Permanent Citation