Projected Area of a Cuboid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
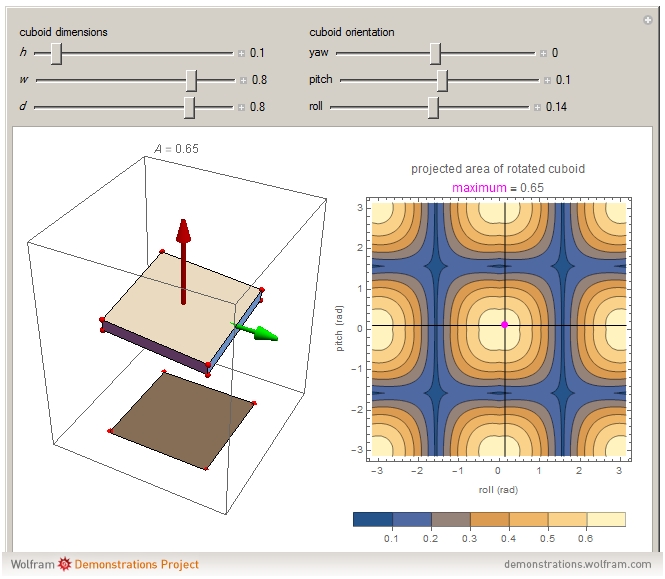
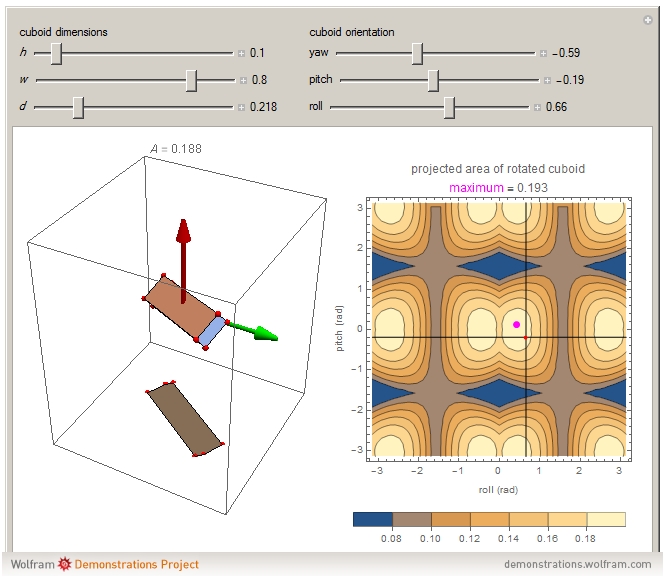
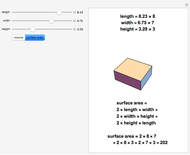
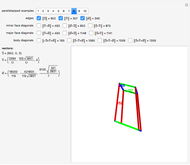
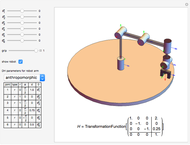
This Demonstration shows the projected area for a cuboid of specified height  , width
, width 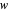 and depth
and depth  after applying roll, pitch and yaw rotations.
after applying roll, pitch and yaw rotations.
Contributed by: Mohammad Sultan and Aaron T. Becker (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
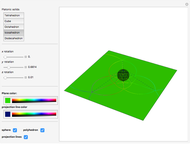
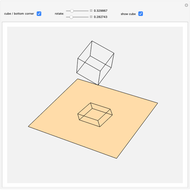
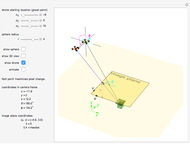
On the left is a 3D cuboid and on the right is the corresponding 2D area for the cuboid when projected into the  -
- plane. The green arrow is in the direction of the positive
plane. The green arrow is in the direction of the positive  axis and the red arrow is the direction of the positive
axis and the red arrow is the direction of the positive  axis.
axis.
The contour plot on the right shows the projected area of the rotated cuboid as a function of pitch and roll angles. The cuboid orientation is determined by the 3D rotation matrix composed by yaw around the initial  axis, followed by by pitch around the initial
axis, followed by by pitch around the initial  axis, and finally by roll around the initial
axis, and finally by roll around the initial  axis. Note that the yaw rotation does not affect the projected area.
axis. Note that the yaw rotation does not affect the projected area.
The projected area can be found in several ways. One method is to project the vertices of the cuboid into 2D and calculate the area of the 2D polygon formed by the convex hull of these vertices. However, this Demonstration uses a Graham scan to find the convex hull.
Alternately, the area can be directly computed from the  ,
, 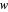 and
and  dimensions and the roll and pitch angles:
dimensions and the roll and pitch angles:
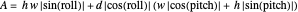 .
.
This function is reflected along the borders of {{0,π/2},{0,π/2}}, and has a maximum of d2 h2+d2 w2+h2 w2 at roll = ArcCos[d h2+w2d2 h2+d2 w2+h2 w2] and pitch = ArcTan[w,h]. The minimum is found at the one of the corners of the set {{0,π/2},{0,π/2}}, and is the minimum of {d·w, h·w, d·h}.
Reference
[1] Mathematics Stack Exchange. "Orthogonal Projection Area of a 3-d Cube." (Aug 20, 2021) math.stackexchange.com/questions/2725780/orthogonal-projection-area-of-a-3-d-cube.
Permanent Citation