Projected Areas of Cylinder and Cone

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
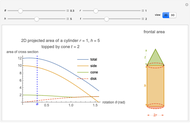
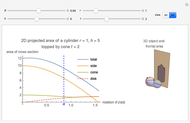
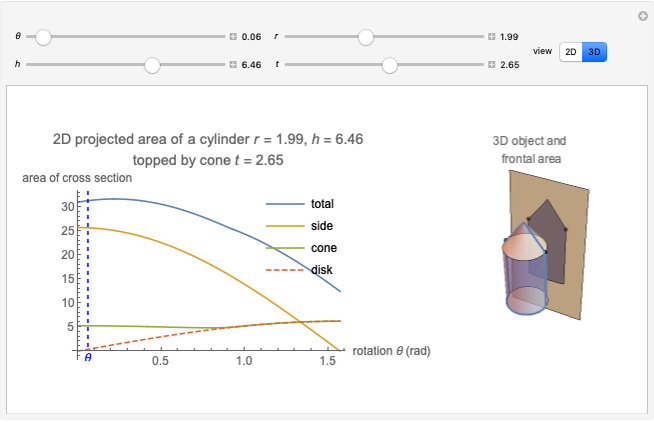
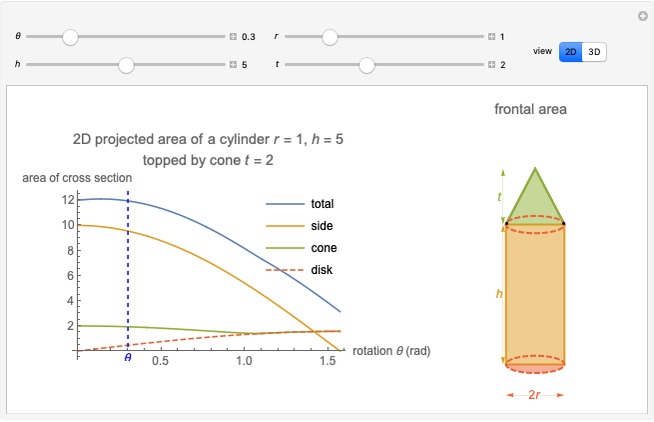
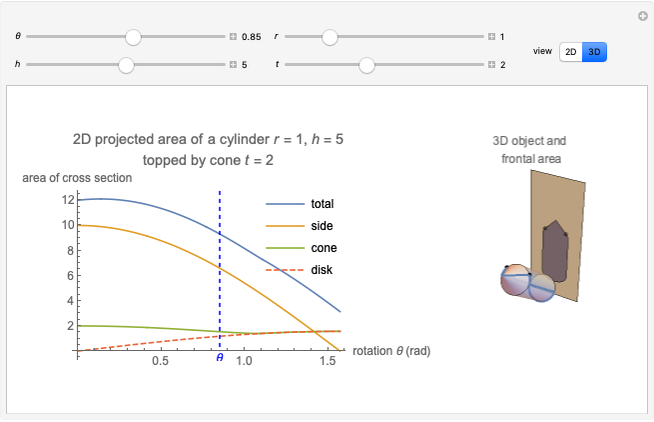
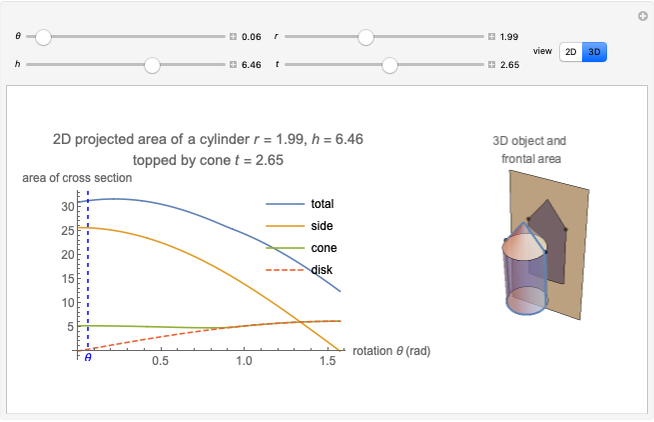
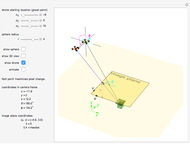
This Demonstration calculates the projected area of a cylinder topped by a cone. This represents the frontal area for fluid flow incident on the cylinder.
Contributed by: Aaron T. Becker and Yitong Lu (January 2021)
Open content licensed under CC BY-NC-SA
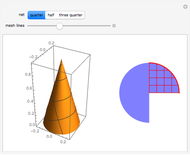
Snapshots
Details
Consider a cylinder of radius  and height
and height  rotated with respect to the flow direction of a fluid by
rotated with respect to the flow direction of a fluid by  about an axis parallel to the base. The frontal area of the cylinder is the area perpendicular to the flow direction. If this shape is projected onto the 2D plane, the resulting 2D area is
about an axis parallel to the base. The frontal area of the cylinder is the area perpendicular to the flow direction. If this shape is projected onto the 2D plane, the resulting 2D area is
 .
.
If  , this is just the rectangle
, this is just the rectangle  . When
. When  , the area is that of the circular end cap
, the area is that of the circular end cap  .
.
A right cone with radius  and height
and height  is more complicated. If
is more complicated. If  , the projected area is just the triangle
, the projected area is just the triangle  . When
. When  , the area is that of the circular base
, the area is that of the circular base  . If
. If  , the cone is rotated so far that the tip of the cone is contained within the projection of the base, so the area is
, the cone is rotated so far that the tip of the cone is contained within the projection of the base, so the area is  , which is the circular base area multiplied by
, which is the circular base area multiplied by  .
.
Otherwise, the area is composed of the union of the ellipse projected by the base of the cone and a triangle from the apex of the cone to points tangent to this ellipse.
These tangent points can be computed by solving for the line that passes through the projection of the apex of the cone  and touches the ellipse at just one point. The tangent points (shown as black points) are
and touches the ellipse at just one point. The tangent points (shown as black points) are
 .
.
The resulting area of the cone is
 .
.
The frontal area is the reference area often used for calculating the coefficient of drag, and is typically defined as the area of the orthographic projection of the object on a plane perpendicular to the direction of motion.
Permanent Citation