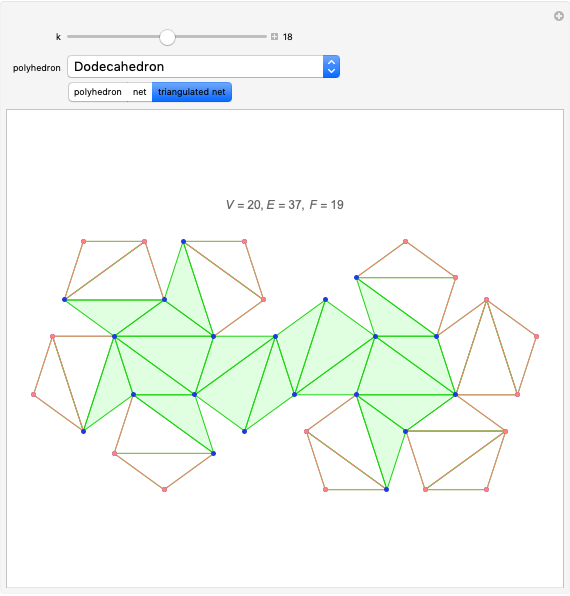
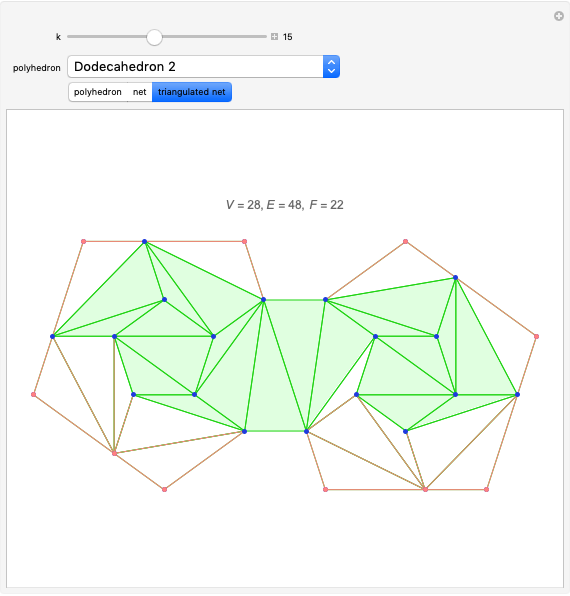
Proving Euler's Polyhedral Formula by Deleting Edges

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
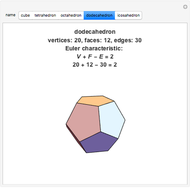
For a polyhedron  , let
, let  be the number of vertices,
be the number of vertices,  the number of edges, and
the number of edges, and  the number of faces. Then Euler's polyhedral formula of 1752 is
the number of faces. Then Euler's polyhedral formula of 1752 is  .
.
Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
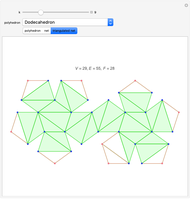
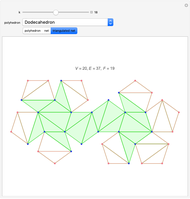
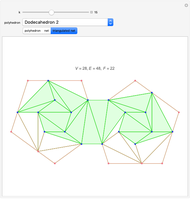
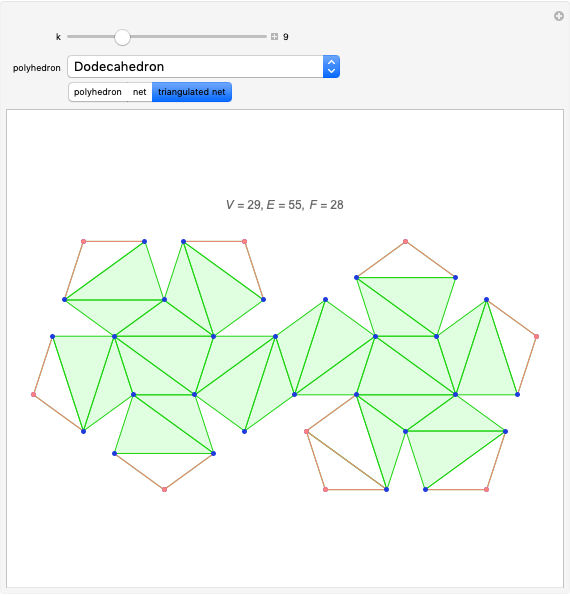
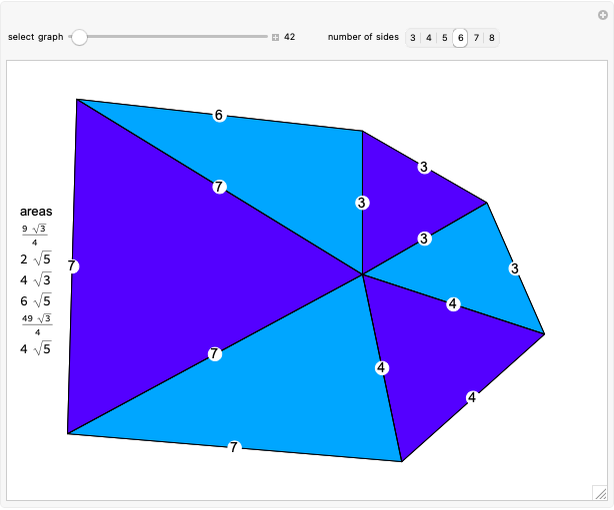
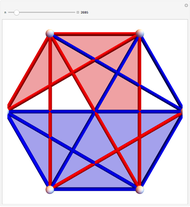
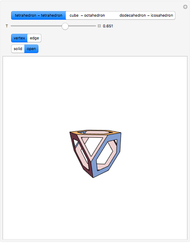
For all the nets here except "Dodecahedron 2", there is always an outside triangle because of the way the nets were constructed.
The proof comes from Abigail Kirk, Euler's Polyhedron Formula.
Unfortunately, there is no guarantee that one can cut along the edges of a spanning tree of a convex polyhedron and flatten out the faces of the polyhedron into the plane to obtain what is called a "net". In fact, Euler's polyhedral formula holds for non-convex polyhedra and examples are known where cutting along the edges of a spanning tree cannot be carried out to get a "net" without faces overlapping. Some non-convex polyhedra cannot have a net.
The proof in this Demonstration, while suggestive, is not actually correct. In this way it is similar to Cauchy's proof of Euler's polyhedral formula that was not correct but was made so when it was proved by Peter Mani that shellings for 3-polytopes existed. Put together with the shelling theorem, it works. Geoffrey Shephard's conjecture as to whether or not a convex 3-polytope has a net is still open.
Euler's formula is treated in [1] D. Richeson, Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton: Princeton University Press, 2008. [2] Nineteen Proofs of Euler's Formula: V-E+F=2.
The most extensive source of information about folding and unfolding problems is [3] E. Demaine and J. O'Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Cambridge: Cambridge University Press, 2007. They discuss the nature of Shephard's conjecture and evidence for and against it.
Thanks to Joseph Malkevitch for the comments and references.
Permanent Citation