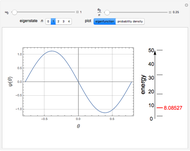
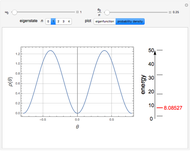
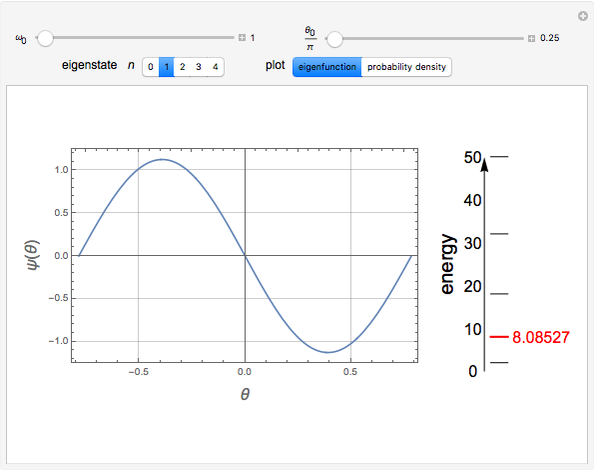
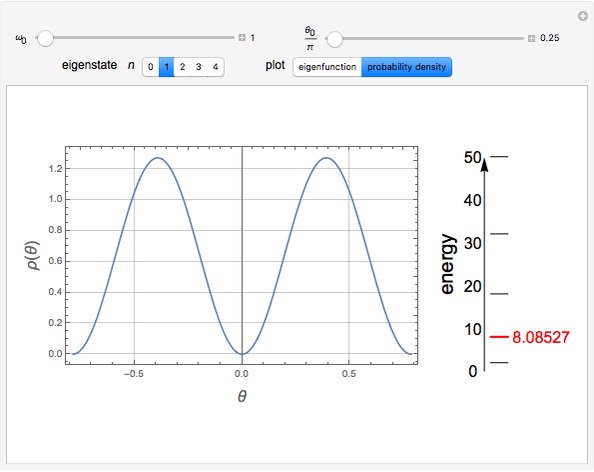
Quantum Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
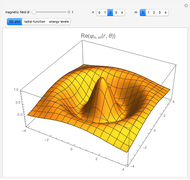
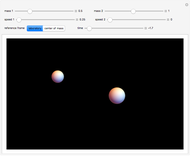
For an idealized classical pendulum consisting of a point mass  attached to a massless rigid rod of length
attached to a massless rigid rod of length  attached to a stationary pivot, in the absence of friction and air resistance, the energy is given by
attached to a stationary pivot, in the absence of friction and air resistance, the energy is given by
Contributed by: S. M. Blinder (January 2019)
Open content licensed under CC BY-NC-SA
Details
References
[1] A. Beléndez, C. Pascual, D. I. Méndez, T. Beléndez and C. Neipp, "Exact Solution for the Nonlinear Pendulum," Revista Brasileira de Ensino de Física, 29(4), 2007 pp. 645–648. doi:10.1590/S1806-11172007000400024.
[2] T. Pradhan and A. V. Khare, "Plane Pendulum in Quantum Mechanics," American Journal of Physics, 41(1), 1973 pp. 59–66. doi:10.1119/1.1987121.
Snapshots
Permanent Citation