Landau Levels in a Magnetic Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
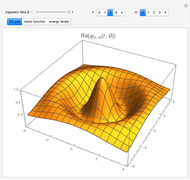
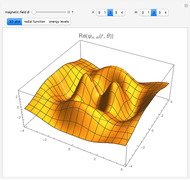
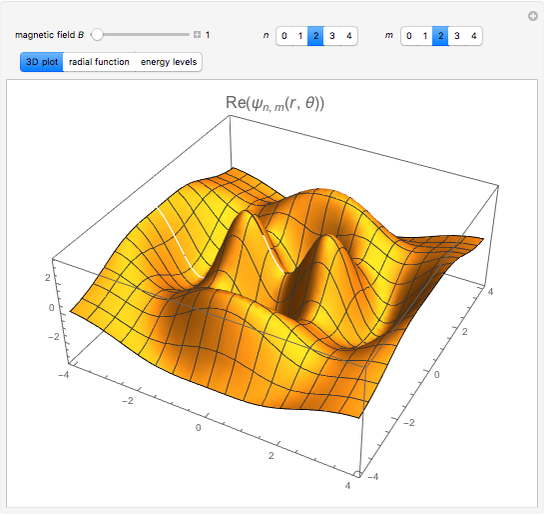
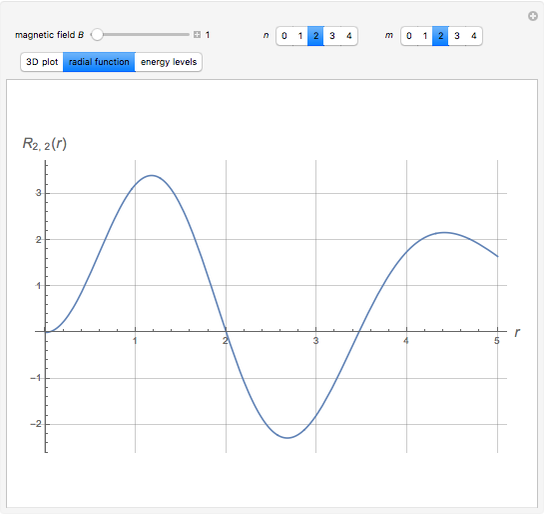
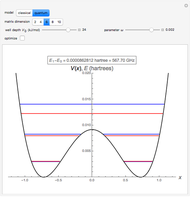
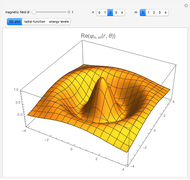
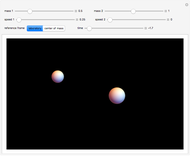
This Demonstration considers the quantum-mechanical system of a free electron in a constant magnetic field, with definite values of the linear and angular momentum in the direction of the field. The wavefunction is plotted in a plane normal to the magnetic field. The corresponding energies are the equally spaced Landau levels, similar to the energies of a harmonic oscillator. These results find application in the theory of the quantum Hall effects.
[more]
Contributed by: S. M. Blinder (December 2018)
Open content licensed under CC BY-NC-SA
Details
The nonrelativistic Hamiltonian for an electron in a magnetic field  , where
, where  is vector potential, is given by
is vector potential, is given by
 ,
,
where  and
and  are the mass and charge of the electron, respectively. We also make use of the Coulomb gauge condition
are the mass and charge of the electron, respectively. We also make use of the Coulomb gauge condition  .
.
For a constant field in the  direction,
direction,  , it is convenient to work in cylindrical coordinates,
, it is convenient to work in cylindrical coordinates,  . With a convenient choice of gauge, the vector potential can be represented by
. With a convenient choice of gauge, the vector potential can be represented by
 ,
,
 .
.
This gives
 .
.
The Schrödinger equation for  is given by
is given by
 .
.
The equation is separable in cylindrical coordinates, and we can write
 ,
,

for definite values of the angular and linear momenta. We consider only angular momentum anticlockwise about the  axis. We set
axis. We set  and consider only motion in a plane perpendicular to the magnetic field. Introducing atomic units
and consider only motion in a plane perpendicular to the magnetic field. Introducing atomic units  , the radial equation reduces to
, the radial equation reduces to
 .
.
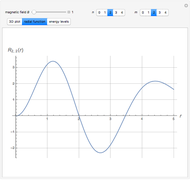
The solution with the correct boundary conditions as  is given by
is given by
 ,
,
where  is an associated Laguerre polynomial. The corresponding energy eigenvalues are
is an associated Laguerre polynomial. The corresponding energy eigenvalues are
 .
.
These are the well-known Landau levels, which are equivalent to the levels of a two-dimensional harmonic oscillator with
 .
.
Recall that

is the cyclotron frequency for an electron in a magnetic field.
References
[1] L. D. Landau and E. M. Lifshitz, Quantum Mechanics: Non-relativistic Theory, 2nd ed., Oxford: Pergamon Press, 1965, pp. 424ff.
[2] D. ter Haar (ed. and tr.), Problems in Quantum Mechanics, 3rd ed., London: Pion, 1975 pp. 38, 254ff.
Snapshots
Permanent Citation