Analogies between Kinematics of Linear and Angular Motion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
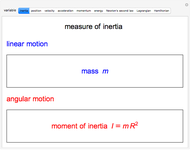
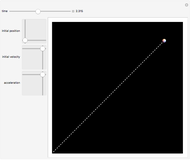
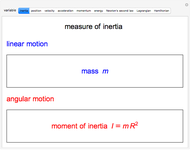
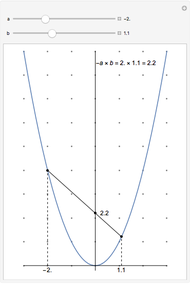
The dynamical variables describing one-dimensional linear and angular (including circular) motion show systematic analogous relationships with one another. For angular motion, the inertial variable analogous to mass  for linear motion is the moment of inertia, given by
for linear motion is the moment of inertia, given by  , where
, where  is the instantaneous radius of curvature. The configuration variable for linear motion is
is the instantaneous radius of curvature. The configuration variable for linear motion is  , while that of angular motion is
, while that of angular motion is  . From these the other dynamical variables for velocity, acceleration, momentum and energy can be built. We also show the forms of Newton's second law and the Lagrangian and Hamiltonian functions,
. From these the other dynamical variables for velocity, acceleration, momentum and energy can be built. We also show the forms of Newton's second law and the Lagrangian and Hamiltonian functions,  and
and  , respectively. The potential energy is represented by the function
, respectively. The potential energy is represented by the function  or
or  . The force and torque for conservative systems are given by
. The force and torque for conservative systems are given by  and
and  .
.
Contributed by: S. M. Blinder (October 2018)
Open content licensed under CC BY-NC-SA
Details
Reference
[1] J. S. Walker, Physics, Vol. 1, 3rd ed., San Francisco: Benjamin Cummings, 2007 Chapter 10.
Snapshots
Permanent Citation