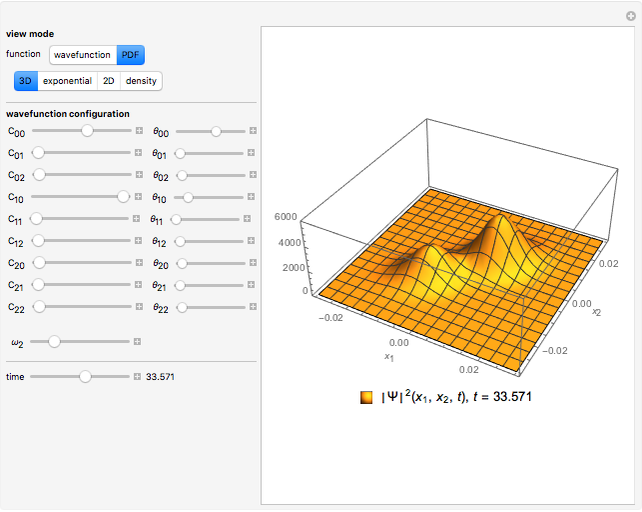
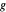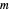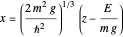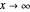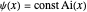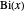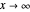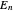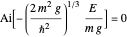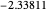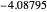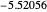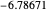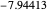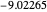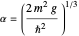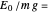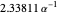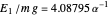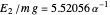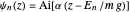Quantum Mechanics of a Bouncing Ball

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
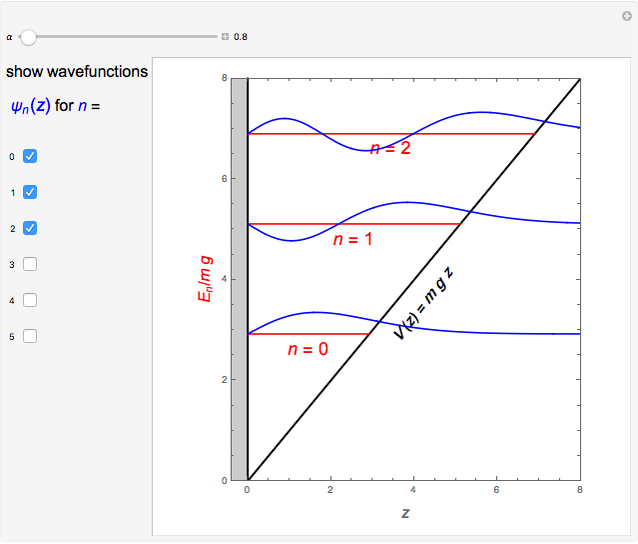
The Schrödinger equation can be written 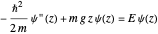 , where
, where 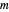 is the mass of the ball (idealized as a point mass),
is the mass of the ball (idealized as a point mass), 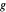 is the acceleration of gravity, and
is the acceleration of gravity, and  is the vertical height (with ground level taken as
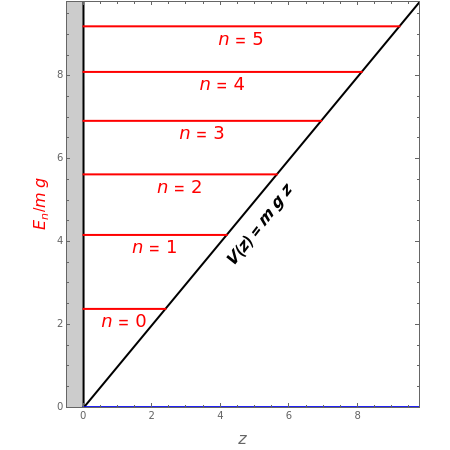
is the vertical height (with ground level taken as 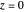 ). For perfectly elastic collisions, the potential energy at
). For perfectly elastic collisions, the potential energy at 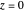 can be assumed infinite:
can be assumed infinite: 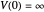 , leading to the boundary condition
, leading to the boundary condition 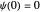 . Also, we should have
. Also, we should have 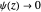 as
as 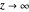 .
.
Contributed by: S. M. Blinder (January 2012)
Open content licensed under CC BY-NC-SA
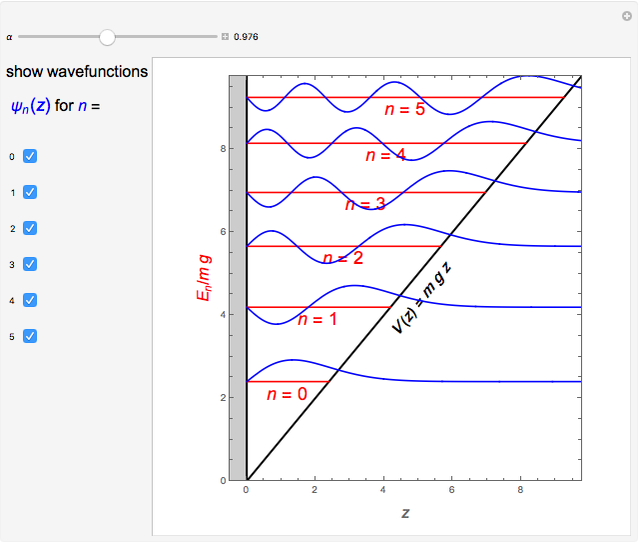
Snapshots
Details
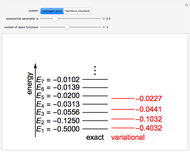
The semiclassical phase integral gives quite accurate values of the energies. Evaluate these using  (the added fraction is
(the added fraction is  , rather than the more common
, rather than the more common  , because one turning point is impenetrable). The integral is explicitly given by
, because one turning point is impenetrable). The integral is explicitly given by 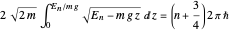 , leading to
, leading to  . The first six numerical values are {2.32025,4.08181,5.51716,6.78445,7.94249,9.02137}, compared with the corresponding exact results from the Schrödinger equation {2.33811,4.08795,5.52056,6.78671,7.94413,9.02265}.
. The first six numerical values are {2.32025,4.08181,5.51716,6.78445,7.94249,9.02137}, compared with the corresponding exact results from the Schrödinger equation {2.33811,4.08795,5.52056,6.78671,7.94413,9.02265}.
Reference
D. ter Haar, ed., Problems in Quantum Mechanics, 3rd ed., London: Pion Ltd., 1975 pp. 6, 98-105.
Permanent Citation