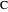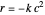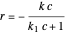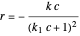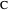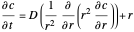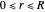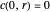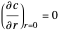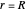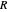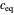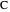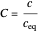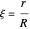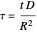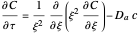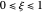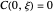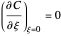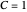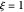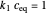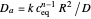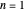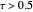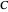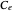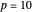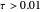Nonlinear reaction diffusion problems expressed mathematically as boundary value problems (ODEs or elliptic PDEs) or initial value problems (parabolic PDEs) are often encountered in chemical engineering applications. A popular numerical method for solving such problems is orthogonal collocation, which reduces the problem to either a system of nonlinear algebraic equations or a system of nonlinear ODEs in time [1, 2]. The accuracy of the method depends on the number of collocation points selected.
In this Demonstration we evaluate the accuracy of the collocation method for studying a family of time-dependent reaction-diffusion problems. We assess the accuracy by comparing the collocation method with the method of lines using NDSolve.
The reaction takes place in a spherical liquid drop. Species 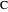 is absorbed, then diffuses and undergoes a decomposition reaction in the interior of the drop. We consider the following possible rates of reaction for the decomposition reaction. The four models are:
is absorbed, then diffuses and undergoes a decomposition reaction in the interior of the drop. We consider the following possible rates of reaction for the decomposition reaction. The four models are:
(1) first-order reaction:  ,
,
(2) second-order reaction: 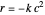 ,
,
(3) Langmuir-like kinetics 1: 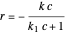 ,
,
(4) Langmuir-like kinetics 2: 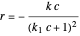 ,
,
where  and
and  are appropriate rate constants.
are appropriate rate constants.
The concentration of species  is taken to be a function of
is taken to be a function of  only. (In the following IC, BC1, and BC2 stand for initial and boundary conditions.) The number balance for
only. (In the following IC, BC1, and BC2 stand for initial and boundary conditions.) The number balance for 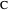 implies:
implies:
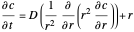 ,
, 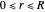 ,
,
IC: 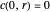 ,
,
BC1: 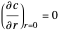 ,
,
BC2:  at
at 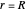 ,
,
where 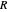 is the radius of the drop, taken to be constant during the reaction, and
is the radius of the drop, taken to be constant during the reaction, and 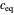 is the concentration of species
is the concentration of species 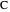 absorbed at the surface of the drop.
absorbed at the surface of the drop.
Dimensionless Form
For the analysis we define the following dimensionless variables:
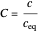 ,
, 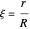 ,
, 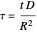 .
.
In dimensionless form, the PDE for the first-order reaction kinetics becomes:
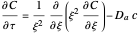 ,
, 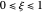 ,
,
IC: 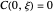 ,
,
BC1: 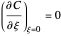 ,
,
BC2: 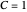 at
at 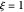 .
.
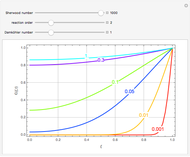
For convenience, we set 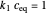 so that the problem depends on a single parameter
so that the problem depends on a single parameter 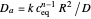 , the Damköhler number (where
, the Damköhler number (where 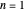 for kinetic models 1, 3, and 4 and
for kinetic models 1, 3, and 4 and 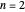 for model 2). When
for model 2). When 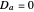 , there is no reaction.
, there is no reaction.
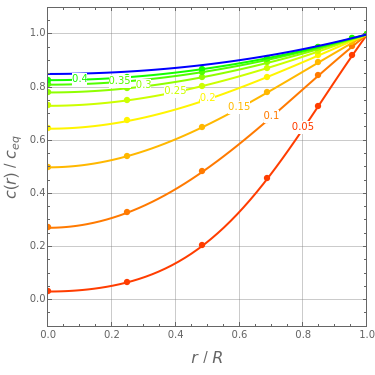
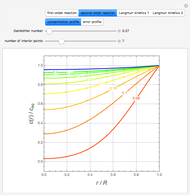
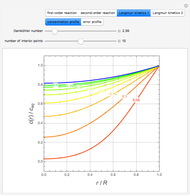
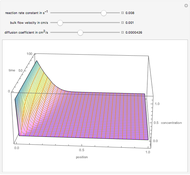
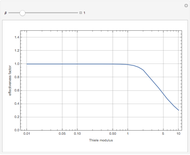
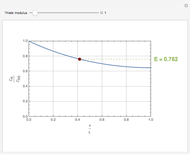
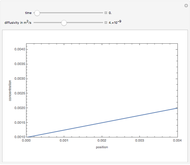
The orthogonal collocation method is based on Jacobi polynomials that reduce the PDE to a system of nonlinear ODEs that are then solved at the collocation points using NDSolve. You can vary the number of interior collocation points and the value of the Damköhler number. This Demonstration plots the dimensionless concentration versus the dimensionless radial position for various values of the dimensionless time using different colors. The colored dots represent the solutions at the collocation points. The colored curves are the predictions found when Mathematica's NDSolve is applied to the nonlinear PDE directly. The blue curve shows the behavior of the concentration at a steady state. This curve was obtained by solving the corresponding boundary value problem using a shooting technique. It is found that a steady state is reached for 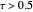 for the range of Damköhler numbers studied.
for the range of Damköhler numbers studied.
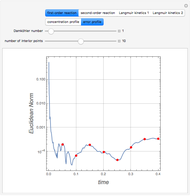
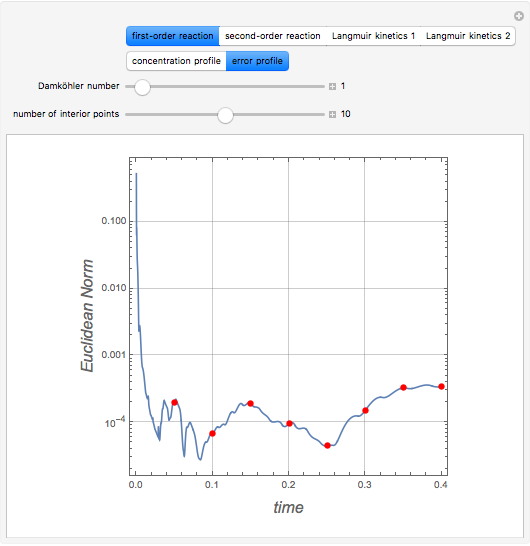
To quantify the accuracy of the collocation method we compute the Euclidean norm of the error for  collocation points given by:
collocation points given by:  where
where 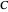 and
and 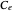 are the solutions obtained using orthognal collocation and NDSolve. This error is plotted as a function of time on the error plot. The red dots denote the times used in concentration versus radial position plots. As the number of collocation points is increased, the Euclidian norm in the error plot is reduced. For
are the solutions obtained using orthognal collocation and NDSolve. This error is plotted as a function of time on the error plot. The red dots denote the times used in concentration versus radial position plots. As the number of collocation points is increased, the Euclidian norm in the error plot is reduced. For 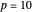 and
and 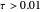 ,
, 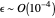 .
.
[less]