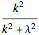Schrödinger Equation for a One-Dimensional Delta Function Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
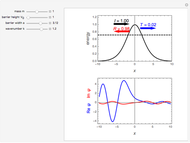
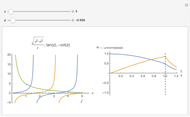
After the free particle, the most elementary example of a one-dimensional time-independent Schrödinger equation is conceptually that of a particle in a delta function potential:  (in units with
(in units with  ). For an attractive potential, with
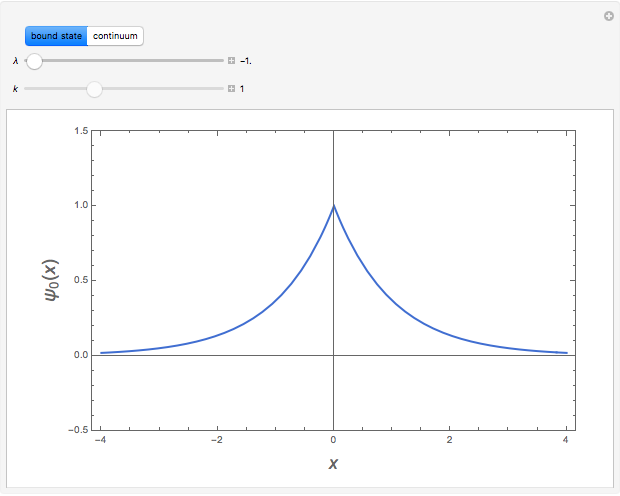
). For an attractive potential, with  , there is exactly one bound state, with
, there is exactly one bound state, with  and
and  . Note that
. Note that  and
and  . Since the delta function has dimensions of
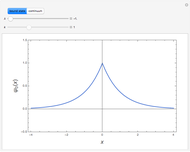
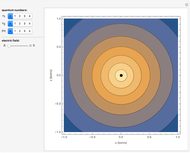
. Since the delta function has dimensions of  , this solution is considered the one-dimensional analog of a hydrogen-like atom. The bound state, in fact, resembles a cross section of a 1
, this solution is considered the one-dimensional analog of a hydrogen-like atom. The bound state, in fact, resembles a cross section of a 1 orbital
orbital  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: wavefunction for the single bound state
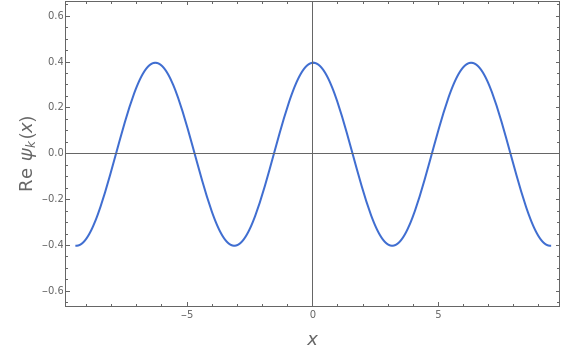
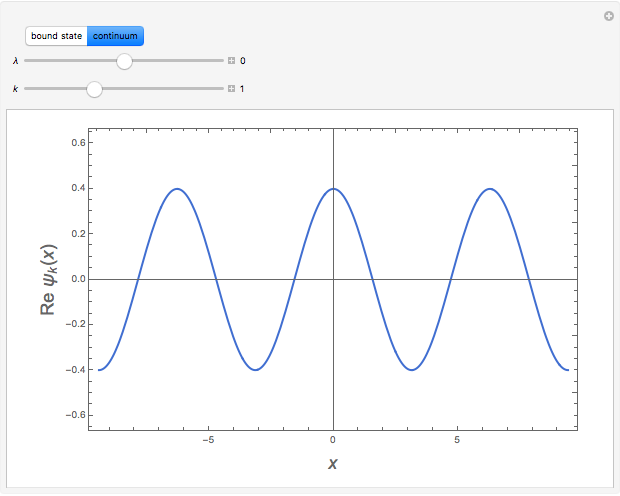
Snapshot 2: unperturbed continuum state, with 
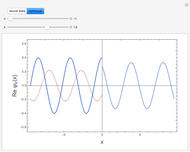
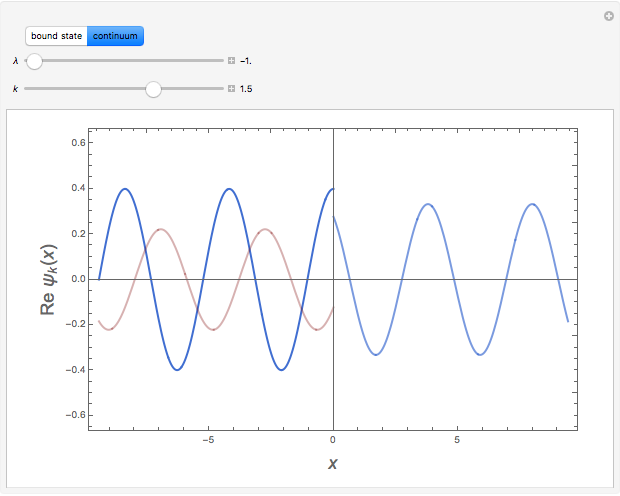
Snapshot 3: scattering state, showing incident, transmitted and reflected waves
Reference: S. M. Blinder, "Green's Function and Propagator for the One-Dimensional Delta Function Potential," Phys. Rev. A, 37(3), 1988 pp. 973–976.
Permanent Citation