Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Sliding to the Fermat Point

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

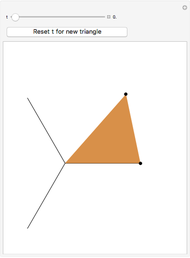
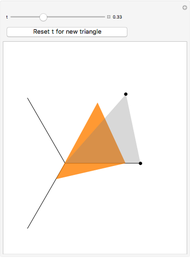
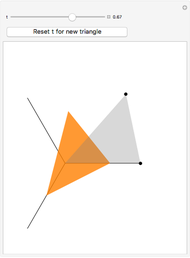
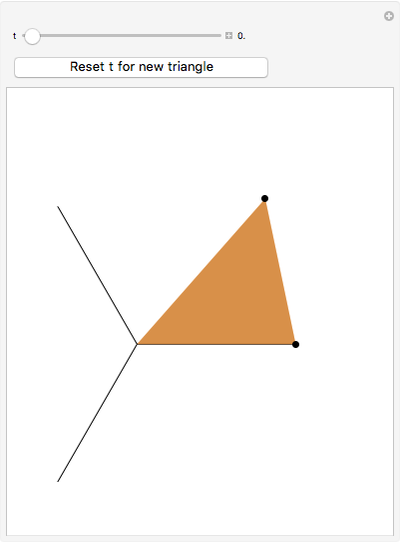
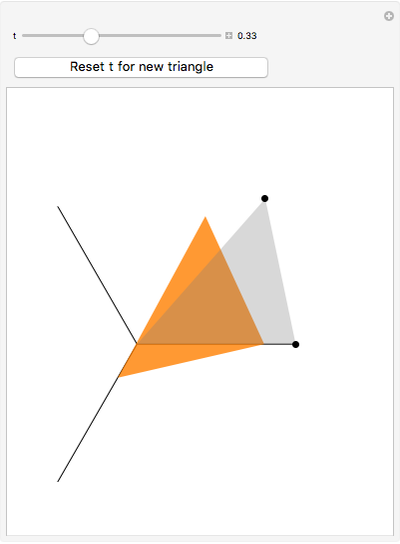
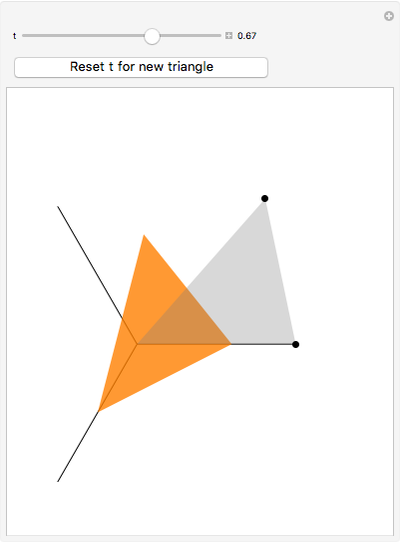
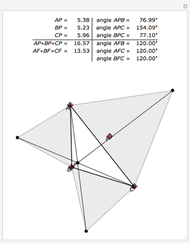
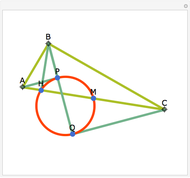
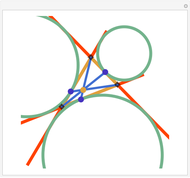
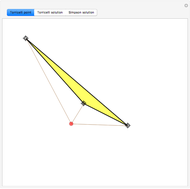
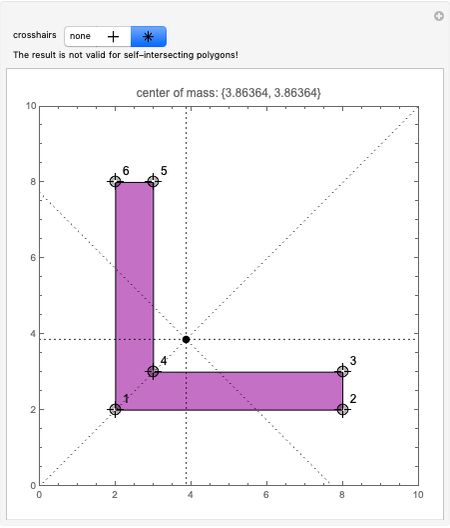
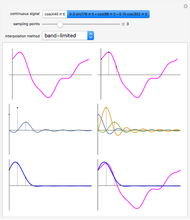
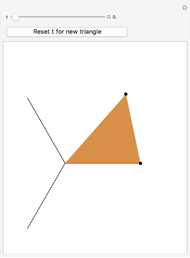
The point that minimizes the sum of the distances to the vertices of a triangle is the Fermat point. If the triangle has no angle greater than or equal to then the Fermat point is an interior point. In this case the angle at the Fermat point between any two vertices is .

[more]

How could you use this information to actually find the Fermat point? Define your triangle by moving the two points and think about the question before moving the slider.

As the slider is adjusted from to the triangle moves into a position so that the Fermat point is at the origin.

[less]

Contributed by: Sijia Liang and Bruce Atwood (July 2011)
(Beloit College)
Based on work by: Kent E. Morrison
Open content licensed under CC BY-NC-SA

Snapshots

Details

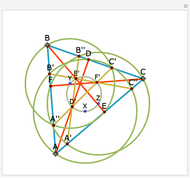
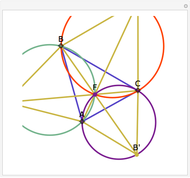
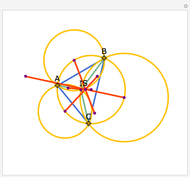
You might want to explore why the segments connecting any two vertices to the Fermat point form an angle of . This can be shown geometrically or by using calculus. Other Demonstrations illustrate geometric solutions, and a calculus solution is given by P. N. Bajaj, "A Note on Steiner's Problem," Mathematics Magazine, 40(5), 1967, p. 273.

This Demonstration is based on: Kent E. Morrison, "The FedEx Problem," The College Mathematics Journal, 41(3), 2010, pp. 222–232.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send