The Polar Planimeter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
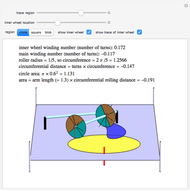
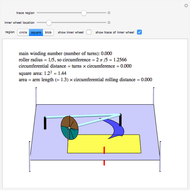
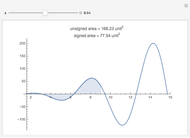
The polar planimeter is a device that measures the area of a plane region by tracing out its boundary. The mechanism has two arms, a fixed anchor point, a freely moving elbow, a needle that traces the boundary of the region counterclockwise, and a wheel whose orientation is perpendicular to the elbow-to-needle arm. If the distance from the elbow to the needle is  , then the net distance rolled by the wheel is the area divided by
, then the net distance rolled by the wheel is the area divided by  . This Demonstration shows two possible locations of the wheel: at the needle, or at an arbitrary point on the elbow-to-needle arm (which is how a real planimeter works). The inner wheel traces out a curve that is a morph between the path of the needle (the region being measured) and the path of the elbow (an arc of a circle).
. This Demonstration shows two possible locations of the wheel: at the needle, or at an arbitrary point on the elbow-to-needle arm (which is how a real planimeter works). The inner wheel traces out a curve that is a morph between the path of the needle (the region being measured) and the path of the elbow (an arc of a circle).
Contributed by: Bruce Atwood (Beloit College) and Stan Wagon (Macalester College) (June 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The planimeter's correctness can be justified by Green's theorem, which equates the tangential line integral of a vector field around a curve to the double integral of the curl of a vector field. Thus the distance traveled by the rolling wheel is a line integral that equals the double integral over the region of the curl of the relevant vector field. Letting  denote the elbow and
denote the elbow and  the needle, the vector field in question is
the needle, the vector field in question is  . The curl of
. The curl of  is 2 and the curl of
is 2 and the curl of  turns out to be
turns out to be  , so the total curl is
, so the total curl is  . To find
. To find  explicitly let
explicitly let  and combine that with
and combine that with  . The inner wheel, which can be placed anywhere on the elbow-to-needle arm, rolls differently than a wheel at the end of the arm, but the total rolling is the same. This can be proved by looking at the vector from the wheel's location to the needle and observing that its total motion is zero. For more information see The Mathematics of Surveying: Part II. The Planimeter.
. The inner wheel, which can be placed anywhere on the elbow-to-needle arm, rolls differently than a wheel at the end of the arm, but the total rolling is the same. This can be proved by looking at the vector from the wheel's location to the needle and observing that its total motion is zero. For more information see The Mathematics of Surveying: Part II. The Planimeter.
Permanent Citation