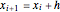Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Graphic Solution of a First-Order Differential Equation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

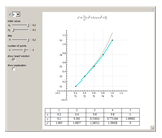
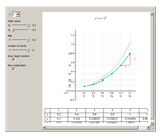
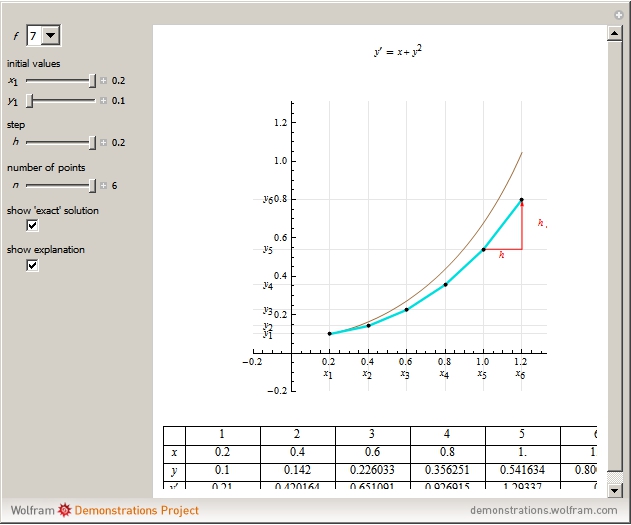
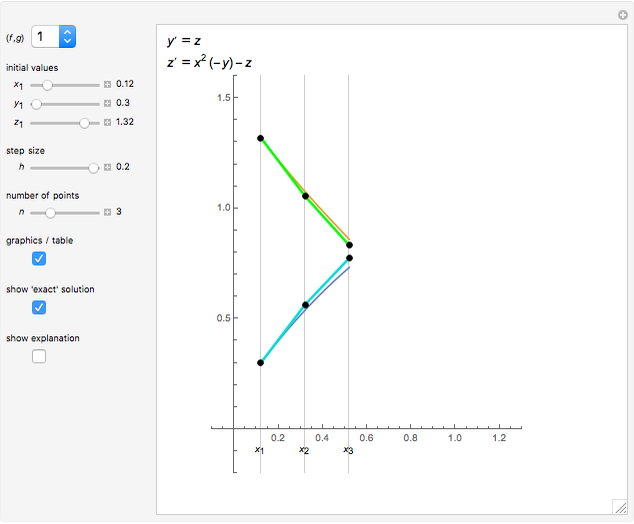
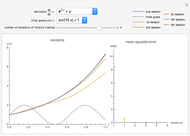
This Demonstration presents Euler's method for the approximate (or graphics) solution of a first-order differential equation with initial condition , .

[more]

The method consists of calculating the approximation of by

,

,

where .

These coordinates determine points , , …, . These points form Euler's polygonal line that is an approximate solution of the problem. The Demonstration compares it with a better solution provided by Mathematica's built-in NDSolve function (brown line).

[less]

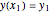Contributed by: Izidor Hafner (January 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] L. Euler, "De Integratione Aequationum Differentialium Per Approximationem," Institutionum Calculi Integralis Volumen Primum, 1768. www.math.dartmouth.edu/~euler/docs/originals/E342sec2ch7.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send